Bài tập dạng dấu của tam thức bậc hai

Bài tập 1: 

a) f(x) = $(4x^{2}-1)(-8x^{2}+x-3)(2x+9)$

- Tam thức $4x^{2}-1$ có hai nghiệm x = $\pm \frac{1}{2}$, a = 4 > 0

- Tam thức $-8x^{2}+x-3$ có $\Delta $ = -47 < 0, hệ số a = -8 < 0 nên luôn luôn âm

- Nhị thức 2x + 9 có nghiệm x = $-\frac{9}{2}$

Ta có bảng xét dấu:

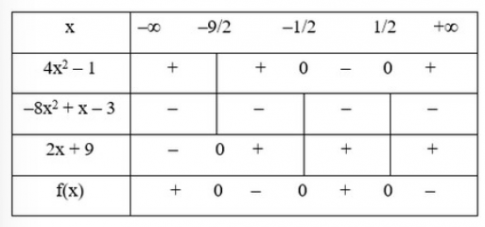
- Từ bảng xét dấu ta có:

f(x) > 0 khi $x\in (-\infty ;-\frac{9}{2})\cup (-\frac{1}{2};\frac{1}{2})$

f(x) = 0 khi $x\in \left \{ -\frac{9}{2};-\frac{1}{2};\frac{1}{2} \right \}$

f(x) < 0 khi $x\in (-\frac{9}{2};-\frac{1}{2})\cup (\frac{1}{2};+\infty )$

b) f(x) = $\frac{(3x^{2}-x)(3-x^{2})}{4x^{2}+x-3}$

- Tam thức $3x^{2}-x$ có hai nghiệm x = 0 và x = $\frac{1}{3}$, hệ số a = 3 > 0

- Tam thức $3-x^{2}$ có hai nghiệm x = $\pm \sqrt{3}$, hệ số a = -1 < 0

- Tam thức $4x^{2}+x-3$ có hai nghiệm x = -1 và x = $\frac{3}{4}$, hệ số a = 4 > 0 

Ta có bảng xét dấu:

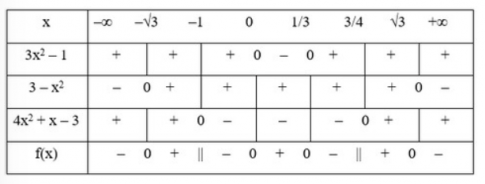
- Từ bảng xét dấu ta có:

f(x) > 0 khi $x\in (-\sqrt{3};-1)\cup (0;\frac{1}{3})\cup (\frac{3}{4};\sqrt{3})$

f(x) = 0 khi $x\in \left \{ \pm \sqrt{3};0;\frac{1}{3} \right \}$

f(x) < 0 khi $x\in(-\infty ;-\sqrt{3})\cup (-1;0)\cup (\frac{1}{3};\frac{3}{4})\cup (\sqrt{3};+\infty )$

f(x) không xác định khi x = -1 và $x=\frac{3}{4}$

Bài tập 2: 

Tam thức bậc hai f(x) = $-5x^{2}+4x+12$ có hai nghiệm là 2 và $-\frac{6}{5}$, hệ số a = -5 < 0 nên: 

$-5x^{2}+4x+12<0\Leftrightarrow \left[\begin{matrix}x &< -\frac{6}{5}\\x&> 2\\\end{matrix}\right.$

Vậy tập nghiệm của bất phương trình đã cho là S = $(-\infty ;-\frac{6}{5})\cup (2;+\infty )$