A. KIẾN THỨC TRỌNG TÂM 

Chủ đề: Mệnh đề 

- Một mệnh đề phải hoặc đúng hoặc sai (không thể vừa đúng vừa sai).

- Mệnh đề phủ định $\bar{P}$ và mệnh đề P là hai phát biểu trái ngược nhau. Nếu P đúng thì $\bar{P}$ sai, còn nếu P sai thì $\bar{P}$ đúng. 

- Mệnh đề "Nếu P thì Q" gọi là mệnh đề kéo theo (kí hiệu: P $\Rightarrow $ Q)

- Mệnh đề Q $\Rightarrow $ P gọi là mệnh đề đảo của mệnh đề P $\Rightarrow $ Q.

- Mệnh đề "P nếu và chỉ nếu Q" gọi là mệnh đề tương đương (kí hiệu: P $\Leftrightarrow $ Q).

Chủ đề: Tập hợp

- Một tập hợp được cho bằng cách liệt kê các phần tử của tập hợp hoặc nêu tính chất đặc trưng cho các phần tử.

- T là tập con của S (kí hiệu: T $\subset $ S hoặc S $\supset $ T) nếu x $\in $ T thì x $\in $ S. 

- Hai tập hợp S và T bằng nhau (kí hiệu: S = T): S = T $\Leftrightarrow $ T $\subset $ S và S $\subset $ T.

- $\mathbb{N}\subset \mathbb{Z}\subset \mathbb{Q}\subset \mathbb{R}$

- Một số tập con thường dùng của $\mathbb{R}$:

+ Khoảng:

(a; b) = {x $\in \mathbb{R}$ | a < x < b}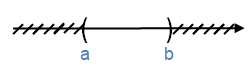 

(a; $+\infty $) = {x $\in \mathbb{R}$ | x > a} 

($-\infty $; b) = {x $\in \mathbb{R}$ | x < b}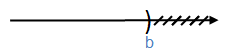 

($-\infty $; $+\infty $)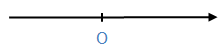                       

+ Đoạn:

[a; b] = {x $\in \mathbb{R}$ | a $\leq $ x $\leq $ b}  

+ Nửa khoảng: 

[a; b) = {x $\in \mathbb{R}$ | a $\leq $ x < b} 

(a; b] = {x $\in \mathbb{R}$ | a < x $\leq $ b}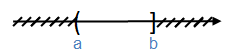 

[a; $+\infty $) = {x $\in \mathbb{R}$ | x $\geq $ a} 

($-\infty $; b] = {x $\in \mathbb{R}$ | x $\leq $ b}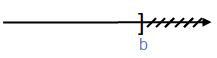 

- Các phép toán trên tập hợp: 

+ Giao hai tập hợp: S $\cap $ T = {x | x $\in $ S và x $\in $ T}

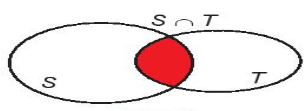
+ Hợp hai tập hợp: S $\cup $ T = {x | x $\in $ S hoặc x $\in $ T}

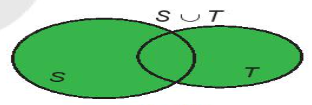
+ Hiệu hai tập hợp: S \ T = {x | x $\in $ S hoặc x $\notin $ T}

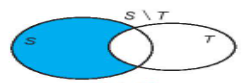
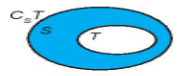
Nếu T $\subset $ S thì S \ T là phần bù ($C_{S}T$)

Chủ đề: Bất phương trình và hệ bất phương trình bậc nhất hai ẩn

- Dạng tổng quát: ax + by $\leq $ c (a, b, c $\in \mathbb{R}$, a và b không đồng thời bằng 0)

- Biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn trên mặt phẳng tọa độ:

+ Vẽ đường thẳng d: ax + by = c trên mặt phẳng tọa độ Oxy

+ Lấy một điểm $M_{0}$ ($x_{0}$; $y_{0}$) không thuộc d

+ Tính a$x_{0}$ + b$y_{0}$ và so sánh với c

+ Nếu a$x_{0}$ + b$y_{0}$ < c thì nửa mặt phẳng bờ d chứa $M_{0}$ là miền nghiệm của bất phương trình. Nếu a$x_{0}$ + b$y_{0}$ > c thì nửa mặt phẳng bờ d không chứa $M_{0}$ là miền nghiệm của bất phương trình.

Chú ý: Miền nghiệm của bất phương trình ax + by < c là miền nghiệm của bất phương trình ax + by $\leq $ c bỏ đi đường miền nghiệm ax + by = c và biểu diễn bằng nét đứt.

- Xác định miền nghiệm của một hệ bất phương trình bậc nhất hai ẩn:

+ Trên cùng một mặt phẳng tọa độ, xác định miền nghiệm của mỗi bất phương trình bậc nhất hai ẩn trong hệ và gạch bỏ miền còn lại.

+ Miền không bị gạch là miền nghiệm của hệ bất phương trình đã cho. 

Chủ đề: Hệ thức lượng trong tam giác

- Giá trị lượng giác của một góc: 

$\tan \alpha =\frac{\sin \alpha }{\cos \alpha } (\alpha \neq 90^{\circ}); \cot \alpha =\frac{\cos \alpha }{\sin \alpha } (\alpha \neq 0^{\circ},\alpha \neq 180^{\circ}); \tan \alpha =\frac{1}{\cot \alpha } (\alpha \neq 0^{\circ};90^{\circ};180^{\circ})$

- Bảng giá trị lượng giác của một số góc đặc biệt:

- Đối với hai góc bù nhau: 

$\sin(180^{\circ}-\alpha )=\sin\alpha $; $\cos(180^{\circ}-\alpha )=-\cos\alpha $

$\tan(180^{\circ}-\alpha )=-\tan\alpha (\alpha \neq 90^{\circ})$; $\cot(180^{\circ}-\alpha )=-\cot\alpha (0^{\circ}< \alpha < 180^{\circ})$

- Định lí Côsin trong tam giác ABC: 

$a^{2}=b^{2}+c^{2}-2bccosA$; $b^{2}=c^{2}+a^{2}-2cacosB$; $c^{2}=a^{2}+b^{2}-2abcosC$

- Định lí Sin trong tam giác ABC: $\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=2R$

- Công thức tính diện tích tam giác ABC:

$S = pr = \frac{(a+b+c)r}{2}$

$S=\frac{1}{2}bcsinA=\frac{1}{2}casinB=\frac{1}{2}absinC$

$S=\frac{abc}{4R}$

$S=\sqrt{p(p-a)(p-b)(p-c)}$ (Công thức Heron)

Chủ đề: Vectơ

- Giá của vectơ là đường thẳng đi qua điểm đầu và điểm cuối của một vectơ.

- Hai vectơ cùng phương nếu có giá song song hoặc trùng nhau. Hai vectơ cùng phương thì chúng cùng hướng hoặc ngược hướng.

- $\vec{a}$ = $\vec{b}$ khi và chỉ khi $\vec{a}$, $\vec{b}$ cùng độ dài và cùng hướng.

- Tổng của hai vectơ: 

+ Quy tắc ba điểm: $\vec{AB}$ + $\vec{BC}$ = $\vec{AC}$

+ Quy tắc hình bình hành: Nếu ABCD là một hình bình hành thì $\vec{AB}$ + $\vec{AD}$ = $\vec{AC}$

- Với ba vectơ $\vec{a}$, $\vec{b}$, $\vec{c}$ tùy ý:

+ Giao hoán: $\vec{a}$ + $\vec{b}$ = $\vec{b}$ + $\vec{a}$

+ Kết hợp: ($\vec{a}$ + $\vec{b}$) + $\vec{c}$ = $\vec{a}$ + ($\vec{b}$ + $\vec{c}$)

+ Vectơ-không: $\vec{a}$ + $\vec{0}$ = $\vec{0}$ + $\vec{a}$ = $\vec{a}$

- Hiệu của hai vectơ: $\vec{MN}$ = $\vec{ON}$ - $\vec{OM}$

- Tích của một vectơ với một số: 

+ Nếu $\vec{a}\neq \vec{0}$, k > 0 thì tích của chúng là một vectơ cùng hướng với $\vec{a}$ và độ dài bằng k|$\vec{a}$|

+ Nếu $\vec{a}\neq \vec{0}$, k < 0 thì tích của chúng là một vectơ ngược hướng với $\vec{a}$ và độ dài bằng (-k)|$\vec{a}$|

- Với hai vectơ $\vec{a}$, $\vec{b}$ và hai số thực k, t, ta có:

k(t$\vec{a}$) = (kt)$\vec{a}$

k($\vec{a}$ + $\vec{b}$) = k$\vec{a}$ + k$\vec{b}$; k($\vec{a}$ - $\vec{b}$) = k$\vec{a}$ - k$\vec{b}$

(k + t)$\vec{a}$ = k$\vec{a}$ + t$\vec{a}$

1$\vec{a}$ = $\vec{a}$; (-1)$\vec{a}$ = -$\vec{a}$

- $\vec{u}(x;y)=\vec{v}(x';y') \Leftrightarrow \begin{cases}x& =x'\\y& = y'\end{cases}$

- Cho hai vectơ $\vec{u}(x;y)$, $\vec{v}(x';y')$, ta có:

$\vec{u}+\vec{v}=(x+x';y+y')$

$\vec{u}-\vec{v}=(x-x';y-y')$

$k\vec{u}=(kx;ky)$, với k $\in \mathbb{R}$

- Với M(x; y) và N(x'; y') thì $\vec{MN}$ = (x' - x; y' - y) và MN = |$\vec{MN}$| = $\sqrt{(x'-x)^{2}+(y'-y)^{2}}$

- Số đo góc $\widehat{BAC}$ là góc giữa $\vec{AB}$ và $\vec{AC}$ hay ($\vec{u};\vec{v}$)

- $\vec{u}.\vec{v}=\left | \vec{u} \right |.\left | \vec{v} \right |.\cos(\vec{u},\vec{v})$

- $\vec{u}\perp \vec{v}\Leftrightarrow \vec{u}.\vec{v}=0$

- $\vec{u}^{2}=\left | \vec{u}^{2} \right |$

- $\vec{u}.\vec{v}=xx'+yy'$

- Với $\vec{u}$, $\vec{v}$, $\vec{w}$ bất kì và mọi số thực k, ta có:

$\vec{u}.\vec{v}=\vec{v}.\vec{u}$ (giao hoán)

$\vec{u}(\vec{v}+\vec{w})=\vec{u}.\vec{v}+\vec{u}.\vec{w}$ (tính chất phân phối đối với phép cộng)

$(k\vec{u}).\vec{v}=k(\vec{u}.\vec{v})=\vec{u}.(k\vec{v})$ 

Chủ đề: Số gần đúng và sai số

- Kí hiệu số đúng: $\bar{a}$, kí hiệu số gần đúng: a

- Sai số tuyệt đối: $\Delta _{a}=\left | a-\bar{a} \right |$

- Sai số tương đối: $\delta _{a}=\frac{\Delta _{a}}{\left | a \right |}$

- Quy tròn số gần đúng:

Với chữ số hàng làm tròn:

+ Giữ nguyên nếu chữ số ngay bên phải nó nhỏ hơn 5

+ Tăng 1 đơn vị nếu chữ số ngay bên phải nó lớn hơn hoặc bằng 5

Với chữ số sau hàng làm tròn

+ Bỏ đi nếu ở phần thập phân

+ Thay bởi các chữ số 0 nếu ở phần số nguyên

Chủ đề: Số trung bình và trung vị. Mốt

- Số trung bình: $\bar{x}=\frac{x_{1}+x_{2}+...+x_{n}}{n}$

- Trung vị

+ Nếu số giá trị là số lẻ thì giá trị chính giữa là trung vị

+ Nếu số giá trị là số chẵn thì trung vị là trung bình cộng của hai giá trị chính giữa

- Tứ phân vị: 

+ Sắp xếp mẫu số liệu tăng dần

+ Tìm trung vị. Giá trị này là $Q_{2}$

+ Tìm trung vị của nửa số liệu bên trái $Q_{2}$. Giá trị này là $Q_{1}$

+ Tìm trung vị của nửa số liệu bên phải $Q_{2}$. Giá trị này là $Q_{3}$

$Q_{1}$, $Q_{2}$, $Q_{3}$ là các tứ phân vị của mẫu số liệu. 

- Mốt là giá trị xuất hiện với tần số lớn nhất

- Khoảng biến thiên R là hiệu số giữa giá trị lớn nhất và giá trị nhỏ nhất trong mẫu số liệu

- Khoảng tứ phân vị: $\Delta _{Q}=Q_{3}-Q_{1}$

- Phương sai: $s^{2}=\frac{(x_{1}-\bar{x})^{2}+(x_{2}-\bar{x})^{2}+...+(x_{n}-\bar{x})^{2}}{n}$

- Độ lệch chuẩn: $s=\sqrt{s^{2}}$