Bài tập dạng vectơ
Dạng 5: Vectơ
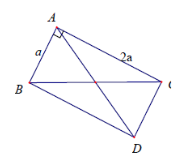
Bài tập 1: Cho tam giác ABC vuông tại A, biết AB = a, AC = 2a. Tính: $\left | \vec{AB}+\vec{AC} \right |$ và $\left | \vec{AB}-\vec{AC} \right |$.
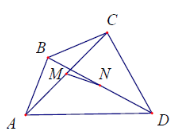
Bài tập 2: Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của hai đường chéo AC và BD. Chứng minh rằng: $\vec{AB}+\vec{CD}=2\vec{MN}$
Bài tập 1:
$\left | \vec{AB}+\vec{AC} \right | = \left | AD \right |=AD=BC=\sqrt{a^{2}+(2a)^{2}}=a\sqrt{5}$
$\left | \vec{AB}-\vec{AC} \right |=\left | CB \right |=CB=a\sqrt{5}$
Bài tập 2:
Ta có: $\vec{MN}=\vec{MA}+\vec{AB}+\vec{BN}$
$\vec{MN}=\vec{MC}+\vec{CD}+\vec{DN}$
Suy ra: $2\vec{MN}=(\vec{MA}+\vec{MC})+\vec{AB}+\vec{CD}+(\vec{BN}+\vec{DN})$
Do đó: $2\vec{MN}=\vec{AB}+\vec{CD}$
Xem toàn bộ: Đề cương ôn tập Toán 10 kết nối tri thức học kì 1
Giải những bài tập khác
Giải bài tập những môn khác
Giải SGK 10 KNTT
Giải SGK 10 CTST
Giải SGK 10 Cánh diều
Giải SBT lớp 10 kết nối tri thức
Giải SBT lớp 10 chân trời sáng tạo
Giải SBT lớp 10 Cánh diều
Giải chuyên đề học tập 10 Kết nối tri thức
Giải chuyên đề học tập 10 Chân trời sáng tạo
Giải chuyên đề học tập 10 Cánh diều
Trắc nghiệm 10 Kết nối tri thức
Trắc nghiệm 10 Chân trời sáng tạo
Trắc nghiệm 10 Cánh diều
Bình luận