Bài tập dạng tập hợp

Bài tập 1: 

Ta có: A = {1; 2; -1}, B = {2; -1}, C = {1; -1}

Do đó: Tập hợp B và C là tập con của tập hợp A. Không có tập hợp nào bằng nhau.

Bài tập 2: 

Gọi A = {Các học sinh nói được tiếng Anh}. Suy ra: Số phần tử của A là 25.

Gọi B = {Các học sinh nói được tiếng Pháp}. Suy ra: Số phần tử của B là 18.

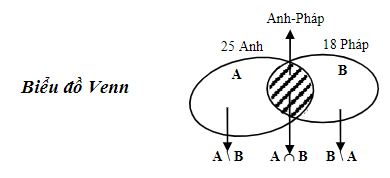
Dựa vào biểu đồ Venn ta có:

- A $\cup $ B là tập hợp các học sinh lớp 10D. Suy ra: A $\cup $ B có 30 phần tử.

- A \ B là tập hợp các học sinh chỉ nói được tiếng Anh.

Ta có: A \ B = (A $\cup $ B) \ B

Suy ra: A \ B có 30 - 18 = 12 phần tử (số học sinh chỉ nói được tiếng Anh)

- B \ A là tập hợp các học sinh chỉ nói được tiếng Pháp

Ta có: B \ A = (A $\cup $ B) \ A

Suy ra: B \ A có 30 - 25 = 5 phần tử (số học sinh chỉ nói được tiếng Pháp)

- A $\cap $ B là số học sinh nói được cả hai thứ tiếng

Ta có: A $\cap $ B = (A $\cup $ B) \ ((A \ B) $\cup $ (B \ A))

Suy ra: A $\cap $ B có 30 - (12 + 5) = 13 phần tử (số học sinh nói được cả hai thứ tiếng Anh và Pháp).