Slide bài giảng toán 8 chân trời bài tập cuối chương 3

Tóm lược nội dung

BÀI TẬP CUỐI CHƯƠNG 3

BÀI TẬP TRẮC NGHIỆM

Bài tập 1 (Trang 88):

Bạn Nam dùng 6 đoạn tre vót thẳng để làm khung diều hình thoi. Trong đó có 2 đoạn tre dài 60 cm và 80 cm để làm hai đường chéo của cái diều, 4 đoạn tre còn lại là 4 cạnh của cái diều. Khi đó tổng độ dài 4 đoạn tre dùng làm cạnh của cái diều hình thoi là

A. 5 m.

B. 1 m.

C. 1,5 m.

D. 2 m.

Trả lời rút gọn:

Đáp án D

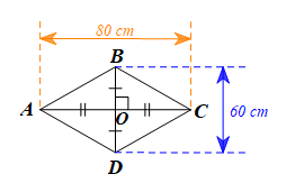
Hình ảnh khung diều hình thoi được mô phỏng bởi hình thoi ABCD có các kích thước như hình vẽ trên.

Do ABCD là hình thoi nên hai đường chéo AC và BD vuông góc với nhau tại trung điểm của mỗi đường.

Suy ra OB =.

Áp dụng định lí Pythagore vào DOAB vuông tại O, ta có:

AB² = OA² + OB² = 40² + 30² = 1 600 + 900 = 2 500 = 50²

Suy ra AB = 50 cm.

Do vậy cạnh của hình thoi có độ dài 50 cm.

Khi đó tổng độ dài 4 đoạn tre dùng làm cạnh của cái diều hình thoi là:

4.50 = 200 (cm) = 2 (m).

Vậy Khi đó tổng độ dài 4 đoạn tre dùng làm cạnh của cái diều hình thoi là 2 m.

Bài tập 2 (Trang 88):

Cho hình thang cân ABCD (AB // CD) có 65°. Số đo góc C là

A. 115°.

B. 95°.

C. 65°.

D. 125°.

Trả lời rút gọn:

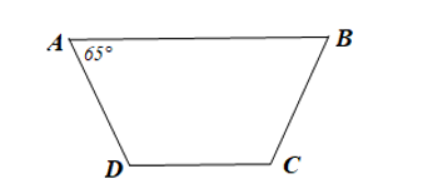
Do ABCD là hình thang cân (AB // CD) nên

Suy ra =

Mặt khác, ABCD là hình thang cân (AB // CD) nên

Bài tập 3 (Trang 88):

Trong các khẳng định sau, khẳng định nào sai?

A. Tứ giác có ba góc vuông là hình chữ nhật.

B. Hình bình hành có một góc vuông là hình chữ nhật.

C. Hình bình hành có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình chữ nhật.

D. Tứ giác có các cạnh đối bằng nhau là hình bình hành.

Trả lời rút gọn:

Đáp án C

Theo tính chất hình bình hành: Hình bình hành có hai đường chéo cắt nhau tại trung điểm của mỗi đường.

Do đó đây là tính chất đã có sẵn của hình bình hành, nên khẳng định C là sai.

Bài tập 4 (Trang 88):

Cho tam giác ABC vuông tại A, đường trung tuyến AM. Biết AB = 8 cm; AC = 15 cm. Độ dài đoạn AM là

A. 8,5 cm.

B. 8 cm.

C. 7 cm.

D. 7,5 cm.

Trả lời rút gọn:

Đáp án A

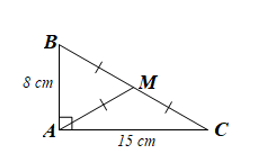
Áp dụng định lí Pythagore vào DABC vuông tại A ta có:

BC² = AB² + AC² = 8² + 15² = 64 + 225 = 289 = 17².

Suy ra BC = 17 cm.

Xét tam giác ABC vuông tại A có đường trung tuyến AM ứng với cạnh huyền BC nên bằng nửa cạnh huyền BC.

Do đó AM=

Bài tập 5 (Trang 88):

Cho hình thoi ABCD có cạnh bằng 13 cm, độ dài đường chéo AC là 10 cm. Độ dài đường chéo BD là

A. 24 cm.

B. 12 cm.

C. 16 cm.

D. 20 cm.

Trả lời rút gọn:

Đáp án A

Do ABCD là hình thoi nên hai đường chéo AC và BD vuông góc với nhau tại trung điểm của mỗi đường.

Suy ra

Áp dụng định lí Pythagore vào OAD vuông tại O, ta có:

Suy ra

Do đó BD = 2OD = 2.12 = 24 (cm).

Bài tập 6 (Trang 88):

Trong các khẳng định sau, khẳng định nào đúng?

A. Hình chữ nhật có hai đường chéo bằng nhau là hình vuông.

B. Hình thoi có hai đường chéo vuông góc là hình vuông.

C. Hình thoi có một góc vuông là hình vuông.

D. Hình chữ nhật có một góc vuông là hình vuông.

Trả lời rút gọn:

Đáp án C

Theo tính chất của hình chữ nhật: Hình chữ nhật có hai đường chéo bằng nhau và có bốn góc vuông. Do đó đây là các tính chất đã có sẵn của hình chữ nhật nên A và D là khẳng định sai.

Theo tính chất của hình thoi: Hình thoi có hai đường chéo vuông góc với nhau. Do đó đây là tính chất đã có sẵn của hình thoi nên B là khẳng định sai.

Hình thoi có một góc vuông là hình vuông. Đây là khẳng định đúng.

Bài tập 7 (Trang 88):

Cho tứ giác ABCD, biết = 60. Khi đó số đo góc C là

A. 120°.

B. 110°.

C. 130°.

D. 80°.

Trả lời rút gọn:

Xét tứ giác ABCD có + + + = 360 (tổng các góc của một tứ giác).

Suy ra =

Do đó = 360 - (

BÀI TẬP TỰ LUẬN

Bài tập 8 (Trang 89):

Cho hình bình hành ABCD. Các điểm E, F thuộc đường chéo AC sao cho AE = EF = FC. Gọi M là giao điểm của BF và CD, N là giao điểm của DE và AB. Chứng minh rằng:

a) M, N theo thứ tự là trung điểm của CD, AB;

b) EMFN là hình bình hành.

Trả lời rút gọn:

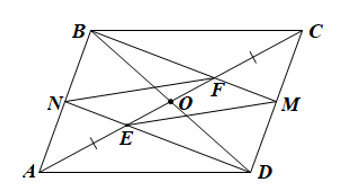
a) 

+ Ta có: nên (1)

Gọi O là giao điểm hai đường chéo AC và BD của hình bình hành.

Khi đó O là trung điểm của AC và BD.

Suy ra (2)

Từ (1) và (2) suy ra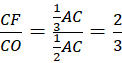

Hay

+ Xét BCD có:

 CO là trung tuyến của tam giác 

mà  

F là trọng tâm của BCD.

Do đó BF hay BM cũng là đường trung tuyến của BCD.

M là trung điểm của CD.

+ CMTT đối với ABD ta có E là trọng tâm của tam giác.

Do đó DE hay DN cũng là đường trung tuyến của ABD.

N là trung điểm của AB.

b) 

+ Do M là trung điểm của CD (câu a)

         N là trung điểm của AB (câu a) nên

Mà (do ABCD là hình bình hành)

Suy ra  

Xét tứ giác BMDN có:

Do đó BMDN là hình bình hành.

+ Ta có E là trọng tâm của ABD nên

          F là trọng tâm của BCD nên  

Mà DN = BM (cmt) 

EN = FM.

+ Xét tứ giác EMFN có:

  (do BM // DN)

EMFN là hình bình hành.

Bài tập 9 (Trang 89):

Cho tam giác ABC cân tại A. Gọi H, D lần lượt là trung điểm của các cạnh BC và AB.

a) Chứng minh rằng tứ giác ADHC là hình thang.

b) Gọi E là điểm đối xứng với H qua D. Chứng minh rằng tứ giác AHBE là hình chữ nhật.

c) Tia CD cắt AH tại M và cắt BE tại N. Chứng minh rằng tứ giác AMBN là hình bình hành.

Trả lời rút gọn:

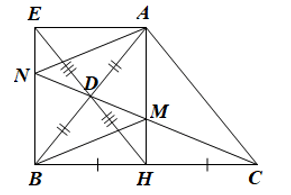
a) + Do ABC cân tại A 

Vì AB = AC A nằm trên đường trung trực của BC.

Vì H là trung điểm của BC H nằm trên đường trung trực của BC.

Do đó AH là đường trung trực của BC .

+ Xét AHB vuông tại H có:

 HD là đường trung tuyến ứng với cạnh huyền AB 

Do đó

+ Tam giác DBH có DB = DH nên là tam giác cân tại D

Suy ra hay

Mà (cmt) 

Mà hai góc này ở vị trí đồng vị nên .

+ Xét tứ giác ADHC có:

 DH // AC 

ADHC là hình thang.

b) Do E là điểm đối xứng với H qua D 

D là trung điểm của HE.

Xét tứ giác AHBE có:

D là trung điểm của AB

D là trung điểm của HE

Mà AB cắt HE tại D

AHBE là hình bình hành.

Mà   (do ) 

hình bình hành AHBE là hình chữ nhật.

c) 

+ Do AHBE là hình chữ nhật AH // BE hay MH // NE

Suy ra (so le trong).

+ Xét MHD và NED có:

(cmt);

DH = DE (do E là điểm đối xứng với H qua D);

(đối đỉnh).

Do đó MHD = NED (g.c.g)

DM = DN (hai cạnh tương ứng).

Hay D là trung điểm của NM.

+ Xét tứ giác AMBN có:

D là trung điểm của AB

D là trung điểm của NM

AB cắt NM tại D 

AMBN là hình bình hành.

Bài tập 10 (Trang 89):

Cho tam giác ABC vuông tại A (AB < AC). Gọi M, N, E lần lượt là trung điểm của AB, AC, BC.

a) Chứng minh rằng tứ giác ANEB là hình thang vuông.

b) Chứng minh rằng tứ giác ANEM là hình chữ nhật.

c) Qua M kẻ đường thẳng song song với BN cắt tia EN tại F. Chứng minh rằng tứ giác AFCE là hình thoi.

d) Gọi D là điểm đối xứng của E qua M. Chứng minh rằng A là trung điểm của DF.

Trả lời rút gọn:

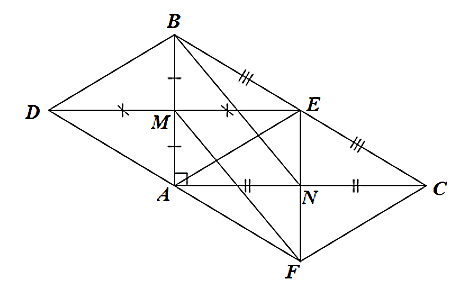
a) + Xét ABC vuông tại A có:

 AE là đường trung tuyến ứng với cạnh huyền BC 

Suy ra

+ Vì EA = EC E nằm trên đường trung trực của AC.

Vì N là trung điểm của AC N nằm trên đường trung trực của AC.

EN là đường trung trực của đoạn thẳng AC

Ta có: BA // EN.

+ Xét tứ giác ANEB có: ANEB là hình thang

Mà  

hình thang ANEB là hình thang vuông.

b) Vì EA = EB E nằm trên đường trung trực của AB.

Vì M là trung điểm của AB M nằm trên đường trung trực của AB.

EM là đường trung trực của AB , 

hay

Xét tứ giác ANEM có:

Mà

ANEM là hình chữ nhật.

c) 

+ Xét tứ giác BMFN có:

(do AB // EN)

BMFN là hình bình hành.

Do đó MB = NF.

Mà AM = MB (do M là trung điểm AB) 

 AM = EN (do ANEM là hình chữ nhật)

Do đó EN = NF hay N là trung điểm của EF.

+ Xét tứ giác AFCE có:

N là trung điểm của AC 

N  là trung điểm của EF 

Mà AC cắt EF tại N AFCE là hình bình hành.

Lại có AFCE là hình thoi.

d) + Do AFCE là hình thoi (câu c) AF // CE và AF = CE.

CMTT câu c, ta cũng có ADBE là hình thoi

+ Ta có

theo tiên đề Euclid ta có: AD và AF trùng nhau hay ba điểm F, A, D thẳng hàng   (1)

+ Ta có  

Mà CE = BE (do E là trung điểm của BC)

AF = AD (2)

Từ (1) và (2) ta có A là trung điểm của DF.

Bài tập 11 (Trang 89):

Cho hình bình hành ABCD có AB = 2AD. Gọi E và F lần lượt là trung điểm của AB và CD, I là giao điểm của AF và DE, K là giao điểm của BF và CE.

a) Chứng minh rằng tứ giác AECF là hình bình hành.

b) Tứ giác AEFD là hình gì? Vì sao?

c) Chứng minh rằng tứ giác EIFK là hình chữ nhật.

d) Tìm điều kiện của hình bình hành ABCD để tứ giác EIFK là hình vuông.

Trả lời rút gọn:

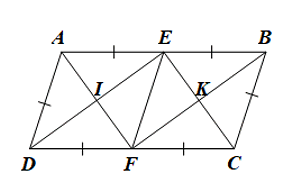
a) + Do ABCD là hình bình hành 

Vì E là trung điểm của AB nên

     F là trung điểm của CD nên

Mà AB = CD (cmt).

Do đó .

+ Xét tứ giác AECF có:

(do AB // CD)

AECF là hình bình hành.

b) Xét tứ giác AEFD có:

AEFD là hình bình hành.

Mặt khác AB = 2AD

Khi đó hình bình hành AEFD là hình thoi.

c) Do AEFD là hình thoi (câu c) nên ta có:

+

+ ED là đường phân giác của góc AEF

CMTT câu c ta cũng có tứ giác BEFC là hình thoi

suy ra

+ EC là đường phân giác của góc BEF

Ta có: 

Mà (hai góc kề bù)

Suy ra

+ Xét tứ giác EIFK có:

  EIFK là hình chữ nhật.

d) Theo câu c, tứ giác EIFK là hình chữ nhật

Do đó để tứ giác EIFK là hình vuông thì IE = IF   (1)

Xét hình thoi AEFD có:

I là trung điểm của AF

I là trung điểm của DE

 AF cắt DE tại I

(2)

Từ (1) và (2) suy ra IA = ID

Xét IAD có:

 IA = ID 

IAD cân tại I (DHNB)

Mà (do )

  IAD vuông cân tại I

Suy ra

Mặt khác AEFD là hình thoi (câu c)

  AF là đường phân giác của góc EAD

Suy ra

Hay

Vậy để tứ giác EIFK là hình vuông thì hình bình hành ABCD cần thêm điều kiện hay ABCD là hình chữ nhật.

Bài tập 12 (Trang 89):

Cho hình bình hành ABCD có AD = 2AB. Từ C vẽ CE vuông góc với AB tại E. Nối E với trung điểm M của AD. Từ M vẽ MF vuông góc với CE tại F, MF cắt BC tại N.

a) Tứ giác MNCD là hình gì?

b) Chứng minh tam giác EMC cân tại M.

c) Chứng minh rằng

Trả lời rút gọn:

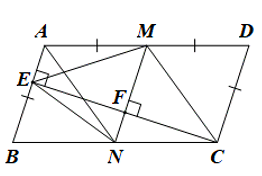
a) + Do ABCD là hình bình hành 

Ta có:

Mà AB // CD 

MN // CD.

Xét tứ giác MNCD có:

MNCD là hình bình hành.

+ Ta có: M là trung điểm của AD 

 hay

Mà

 AB = MD

Mà AB = CD (do ABCD là hình bình hành)

Do đó MD = CD.

+ Hình bình hành MNCD có MD = CD nên MNCD là hình thoi.

b) + Do MNCD là hình thoi

(do AD = BD).

Do

  N là trung điểm của BC.

+ Xét EBC vuông tại E có:

 EN là đường trung tuyến ứng với cạnh huyền BC 

+ Do NE = NC N nằm trên đường trung trực của đoạn thẳng EC

Hay đường trung trực của EC đi qua N và vuông góc với EC.

Lai có NF là đường trung trực của đoạn thẳng BC.

F là trung điểm của EC hay FE = FC.

+ Xét EMF và CMF có:

MF là cạnh chung;

(cmt).

Do đó EMF = CMF (hai cạnh góc vuông).

Suy ra ME = MC (hai cạnh tương ứng)

Xét EMC có:

 ME = MC 

EMC cân tại M.

c) + Vì AB // MN (cma)

  (so le trong)

Ta có EMF = CMF (cmb) 

Do đó

+ Do MNCD là hình thoi MC là đường phân giác của góc DMN

(1)

+ Do DMNC là hình thoi 

(hai góc đối bằng nhau)

Do ABCD là hình bình hành (hai góc đối bằng nhau)

Do đó (2)

Từ (1) và (2) ta có  

hay