Slide bài giảng toán 8 chân trời bài 4: Phân tích đa thức thành nhân tử
Slide điện tử bài 4: Phân tích đa thức thành nhân tử. Kiến thức bài học được hình ảnh hóa, sinh động hóa. Trình bày với các hiệu ứng hiện đại, hấp dẫn. Giúp học sinh hứng thú học bài. Học nhanh, nhớ lâu. Có tài liệu này, hiệu quả học tập của học môn Toán 8 chân trời sáng tạo sẽ khác biệt
Bạn chưa đủ điều kiện để xem được slide bài này. => Xem slide bài mẫu
Tóm lược nội dung
BÀI 4. PHÂN TÍCH ĐA THỨC THÀNH NHÂN TỬ
1. PHƯƠNG PHÁP ĐẶT NHÂN TỬ CHUNG
Hoạt động 1 (Trang 23):
Tính diện tích của nền nhà có bản vẽ sơ lược như Hình 1 theo những cách khác nhau, biết a = 5; b = 3,5 (các kích thước tính theo mét).
Tính theo cách nào nhanh hơn?

Trả lời rút gọn:

Cách 1: Tính tổng diện tích các hình.
Diện tích hình chữ nhật có chiều dài a (m) và chiều rộng b – 1 (m) là: a(b – 1) (m2).
Diện tích hình chữ nhật có chiều dài a (m) và chiều rộng b (m) là: ab (m2).
Diện tích hình chữ nhật có chiều dài a (m) và chiều rộng 4,5 (m) là: 4,5a (m2).
Diện tích của nền nhà là: S = a(b – 1) + ab + 4,5a (m2).
Với a = 5 và b = 3,5 ta có:
S = 5.(3,5 – 1) + 5.3,5 + 4,5.5
= 5 . (3,5 – 1 + 3,5 + 4,5)
= 5 . 10,5
= 52,5 (m2).
Cách 2: Tính chiều dài của nền nhà rồi tính diện tích của nền nhà.
Chiều dài của nền nhà là:
b – 1 + b + 4,5 = 2b + 3,5 (m).
Diện tích của nền nhà là: S = a.(2b + 3,5) (m2).
Với a = 5 và b = 3,5 ta có:
S = 5.(2.3,5 + 3,5) = 5 . 10,5 = 52,5 (m2).
Thực hành 1 (Trang 24):
Phân tích các đa thức sau thành nhân tử:
a) P = 6x – 2x3;
b) Q = 5x3 – 15x2y;
c) R = 3x3y3 – 6xy3z + xy.
Trả lời rút gọn:
a) P = 6x – 2x3
= 2x.3 – 2x.x2
= 2x(3 – x2).
= 2x.(![]() + x).(
+ x).(![]() - x)
- x)
b) Q = 5x3 – 15x2y
= 5x2.x – 5x2.3y
= 5x2(x – 3y).
c) R = 3x3y3 – 6xy3z + xy
= xy.3x2y2 – xy.6y2z + xy.1
= xy.(3x2y2 – 6y2z + 1).
2. PHƯƠNG PHÁP SỬ DỤNG HẰNG ĐẲNG THỨC
Hoạt động 2 (Trang 24):
Tìm biểu thức thích hợp thay vào mỗi chỗ ![]() , từ đó hoàn thành biến đổi sau vào vở để phân tích đa thức sau thành nhân tử:....
, từ đó hoàn thành biến đổi sau vào vở để phân tích đa thức sau thành nhân tử:....
Trả lời rút gọn:
a) 4x2−9=(2x)2−(3)2=(2x−3)(2x+3)
b) x2y2−![]() y2=(xy)2−(
y2=(xy)2−(![]() y)2=(xy−
y)2=(xy−![]() y)( xy+
y)( xy+![]() y)
y)
Thực hành 2 (Trang 24):
Phân tích các đa thức sau thành nhân tử:
a) 9x2 – 16;
b) 4x2 – 12xy + 9y2;
c) t3 – 8;
d) 2ax3y3 + 2a.
Trả lời rút gọn:
a) 9x2 – 16 = (3x)2 – 42
= (3x – 4)(3x + 4).
b) 4x2 – 12xy + 9y2
= (2x)2 – 2.2x.3y + (3y)2
= (2x – 3y)2.
c) t3 – 8 = t3 – 23
= (t – 2)(t2 + t.2 + 22)
= (t – 2)(t2 + 2t + 4).
d) 2ax3y3 + 2a
= 2a.(x3y3 + 1)
= 2a.[(xy)3 + 13]
= 2a(xy + 1)[(xy)2 – xy.1 + 12]
= 2a(xy + 1)(x2y2 – xy + 1).
Vận dụng 1 (Trang 24):
Tìm một hình hộp chữ nhật có thể tích 2x3 – 18x (với x > 3) mà độ dài các cạnh đều là biểu thức chứa x
Trả lời rút gọn:
Ta có: 2x3 – 18x = 2x(x2 – 9)
= 2x(x2 – 32)
= 2x(x – 3)(x + 3)
Vậy hình hộp chữ nhật có thể tích 2x3 – 18x (với x > 3) sẽ có độ dài ba kích thước là 2x, x – 3 và x + 3.
Vận dụng 2 (Trang 24):
Giải đáp câu hỏi ở Hoạt động khởi động (trang 23)
Trả lời rút gọn:
Ta có: 993 – 99 = 99.(992 – 1)
= 99.(992 – 12)
= 99.(99 – 1).(99 + 1)
= 99.98.100
Do đó 993 – 99 chia hết cho cả ba số 98, 99 và 100.
Ta có: n3 – n = n(n2 – 1)
= n.(n – 1).(n + 1)
Do đó n3 – n chia hết cho n, n – 1 và n + 1.
Vậy phát biểu của cả hai bạn đều đúng.
3. PHƯƠNG PHÁP NHÓM HẠNG TỬ
Hoạt động 3 (Trang 24):
Hãy hoàn thành biến đổi sau vào vở để phân tích đa thức thành nhân tử:
a2 + ab + 2a + 2b = (a2 + ab) + (2a + 2b) = …
Em có thể biến đổi theo cách khác để phân tích đa thức trên thành nhân tử không?
Trả lời rút gọn:
a2 + ab + 2a + 2b
= (a2 + ab) + (2a + 2b)
= a(a + b) + 2(a + b)
= (a + b)(a + 2).
Ta có thể biến đổi theo cách khác như sau:
a2 + ab + 2a + 2b
= (a2 + 2a) + (ab + 2b)
= a(a + 2) + b(a + 2)
= (a + 2)(a + b).
Thực hành 3 (Trang 25):
Phân tích các đa thức sau thành nhân tử:
a) a3 – a2b + a – b;
b) x2 – y2 + 2y – 1.
Trả lời rút gọn:
a) a3 – a2b + a – b
= (a3 – a2b) + (a – b)
= a2(a – b) + (a – b)
= (a – b)(a2 + 1).
b) x2 – y2 + 2y – 1
= x2 – (y2 – 2y + 1)
= x2 – (y – 1)2
= (x + y – 1).[x – (y – 1)]
= (x + y – 1)(x – y + 1).
Vận dụng 3 (Trang 25):
Có thể ghép bốn tấm pin mặt trời với kích thước như Hình 2 thành một hình chữ nhật không? Nếu có, tính độ dài các cạnh và diện tích hình chữ nhật đó. Biết a = 0,8; b = 2 (các kích thước tính theo mét).
Trả lời rút gọn:
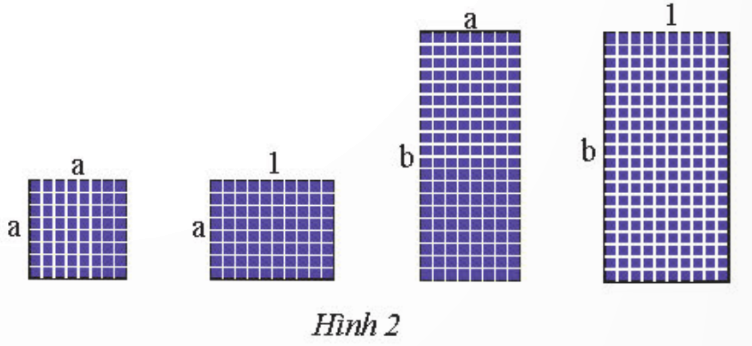
Diện tích tấm pin hình vuông có cạnh bằng a là: a2 (m2).
Diện tích tấm pin hình chữ nhật có chiều dài bằng 1 và chiều rộng bằng a là: a.1 = a (m2).
Diện tích tấm pin hình chữ nhật có chiều dài bằng b và chiều rộng bằng a là: ab (m2).
Diện tích tấm pin hình chữ nhật có chiều dài bằng b và chiều rộng bằng 1 là: b.1 = b (m2).
Tổng diện tích bốn tấm pin mặt trời là:
S = a2 + a + ab + b = (a2 + a) + (ab + b)
= a(a + 1) + b(a + 1)
= (a + 1)(a + b) (m2).
Vậy có thể ghép bốn tấm pin mặt trời với kích thước như Hình 2 thành một hình chữ nhật có chiều rộng là a + 1 (m) và chiều dài là a + b (m), với các tấm pin đã cho theo thứ tự từ trái qua phải được đặt lần lượt các vị trí (1), (2), (3) và (4) theo sơ đồ như hình bên.

Với a = 0,8 (m) và b = 2 (m) ta có:
+ Chiều rộng hình chữ nhật đó là 0,8 + 1 = 1,8 (m).
+ Chiều dài hình chữ nhật đó là 0,8 + 2 = 2,8 (m).
+ Diện tích hình chữ nhật đó là: 1,8 . 2,8 = 5,04 (m2).
BÀI TẬP CUỐI SGK
Bài tập 1 (Trang 25):
Phân tích các đa thức sau thành nhân tử:
a) x3 + 4x;
b) 6ab – 9ab2;
c) 2a(x – 1) + 3b(1 – x);
d) (x – y)2 – x(y – x).
Trả lời rút gọn:
a) x3 + 4x = x.x2 + x.4 = x(x2 + 4).
b) 6ab – 9ab2 = 3ab.2 – 3ab.3b = 3ab(2 – 3b).
c) 2a(x – 1) + 3b(1 – x)
= 2a(x – 1) + 3b[– (x – 1)]
= 2a(x – 1) – 3b(x – 1)
= (x – 1)(2a – 3b).
d) (x – y)2 – x(y – x)
= (x – y)2 + x(x – y)
= (x – y)(x – y + x)
= (x – y)(2x – y).
Bài tập 2 (Trang 25):
Phân tích các đa thức sau thành nhân tử:
a) 4x2 – 1;
b) (x + 2)2 – 9;
c) (a + b)2 – (a – 2b)2.
Trả lời rút gọn:
a) 4x2 – 1 = (2x)2 – 12 = (2x + 1)(2x –1).
b) (x + 2)2 – 9 = (x + 2)2 – 32
= (x + 2 + 3)(x + 2 – 3)
= (x + 5)(x – 1).
c) (a + b)2 – (a – 2b)2
= [(a + b) + (a – 2b)] . [(a + b) – (a – 2b)]
= [a + b + a – 2b] . [a + b – a + 2b]
= (2a – b).3b.
Bài tập 3 (Trang 25):
Phân tích các đa thức sau thành nhân tử:
a) 4a2 + 4a + 1;
b) –3x2 + 6xy – 3y2;
c) (x + y)2 – 2(x + y)z + z2.
Trả lời rút gọn:
a) 4a2 + 4a + 1
= (2a)2 + 2.2a.1 + 12
= (2a + 1)2.
b) –3x2 + 6xy – 3y2
= –3(x2 – 2xy + y2)
= –3(x – y)2.
c) (x + y)2 – 2(x + y)z + z2
= [(x + y) – z]2
= (x + y – z)2.
Bài tập 4 (Trang 25):
Phân tích các đa thức sau thành nhân tử:
a) 8x3 – 1;
b) x3 + 27y3;
c) x3 – y6.
Trả lời rút gọn:
a) 8x3 – 1
= (2x)3 – 13
= (2x – 1)[(2x)2 + 2x.1 + 12]
= (2x – 1)(4x2 + 2x + 1).
b) x3 + 27y3
= x3 + (3y)3
= (x + 3y)[x2 – x.3y + (3y)2]
= (x + 3y)(x2 – 3xy + 9y2).
c) x3 – y6
= x3 – (y2)3
= (x – y2)[x2 + x.y2 + (y2)2]
= (x – y2)(x2 + xy2 + y4).
Bài tập 5 (Trang 25):
Phân tích các đa thức sau thành nhân tử:
a) 4x3 – 16x;
b) x4 – y4;
c) xy2 + x2y + ![]() y3;
y3;
d) x2 + 2x – y2 + 1.
Trả lời rút gọn:
a) 4x3 – 16x
= 4x(x2 – 4)
= 4x(x2 – 22)
= 4x(x + 2)(x – 2).
b) x4 – y4
= (x2)2 – (y2)2
= (x2 + y2)(x2 – y2)
= (x2 + y2)(x + y)(x – y).
c) xy2 + x2y + ![]() y3
y3
= y(xy + x2 + ![]() y2)
y2)
=y[x2+2.x. ![]() y+(
y+(![]() y)2]
y)2]
=y(x+![]() y)2
y)2
d) x2 + 2x – y2 + 1
= (x2 + 2x + 1) – y2
= (x + 1)2 – y2
= (x + 1 + y)(x + 1 – y).
Bài tập 6 (Trang 25):
Phân tích các đa thức sau thành nhân tử:
a) x2 – xy + x – y;
b) x2 + 2xy – 4x – 8y;
c) x3 – x2 – x + 1.
Trả lời rút gọn:
a) x2 – xy + x – y
= (x2 – xy) + (x – y)
= x(x – y) + (x – y)
= (x – y)(x + 1).
b) x2 + 2xy – 4x – 8y
= (x2 + 2xy) – (4x + 8y)
= x(x + 2y) – 4(x + 2y)
= (x + 2y)(x – 4).
c) x3 – x2 – x + 1
= (x3 – x2) – (x – 1)
= x2(x – 1) – (x – 1)
= (x – 1)(x2 – 1)
= (x – 1)(x + 1)(x – 1)
= (x – 1)2(x + 1).
Bài tập 7 (Trang 25):
Cho y > 0. Tìm độ dài cạnh của hình vuông có diện tích bằng 49y2 + 28y + 4.
Trả lời rút gọn:
Giả sử hình vuông có độ dài cạnh bằng a (a > 0), khi đó diện tích của hình vuông là a2.
Tức là 49y2 + 28y + 4 = a2.
Ta phân tích đa thức 49y2 + 28y + 4 thành nhân tử có dạng a2.
49y2 + 28y + 4
= (7y)2 + 2.7y.2 + 22
= (7y + 2)2
Vậy độ dài cạnh của hình vuông có diện tích bằng 49y2 + 28y + 4 là 7y + 2.
