Slide bài giảng toán 8 chân trời bài 2: Tứ giác

Tóm lược nội dung

BÀI 2. TỨ GIÁC

1. TỨ GIÁC

Hoạt động 1 (Trang 63):

Trong các hình tạo bởi bốn đoạn thẳng AB, BC, CD và DA sau đây, hình nào không có hai đoạn thẳng cùng nằm trên một đường thẳng?

Trả lời rút gọn:

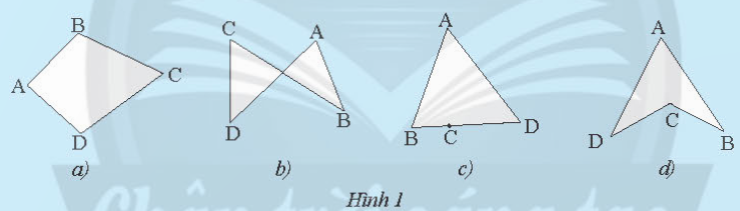
Trong các hình tạo bởi bốn đoạn thẳng AB, BC, CD và DA ở Hình 1a), b), d) không có hai đoạn thẳng cùng nằm trên một đường thẳng.

Hoạt động 2 (Trang 64):

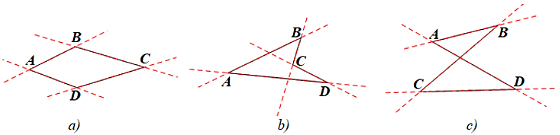
Vẽ các đường thẳng lần lượt chứa mỗi cạnh của các tứ giác sau đây và nêu nhận xét của em về vị trí của các cạnh còn lại của tứ giác đối với mỗi đường thẳng đã vẽ.

Trả lời rút gọn:

Ta vẽ các đường thẳng lần lượt chứa mỗi cạnh của các tứ giác như hình vẽ dưới đây:

Thực hành 1 (Trang 65):

Vẽ tứ giác MNPQ và tìm:

‒ Hai đỉnh đối nhau;

‒ Hai đường chéo;

‒ Hai cạnh đối nhau.

Trả lời rút gọn:

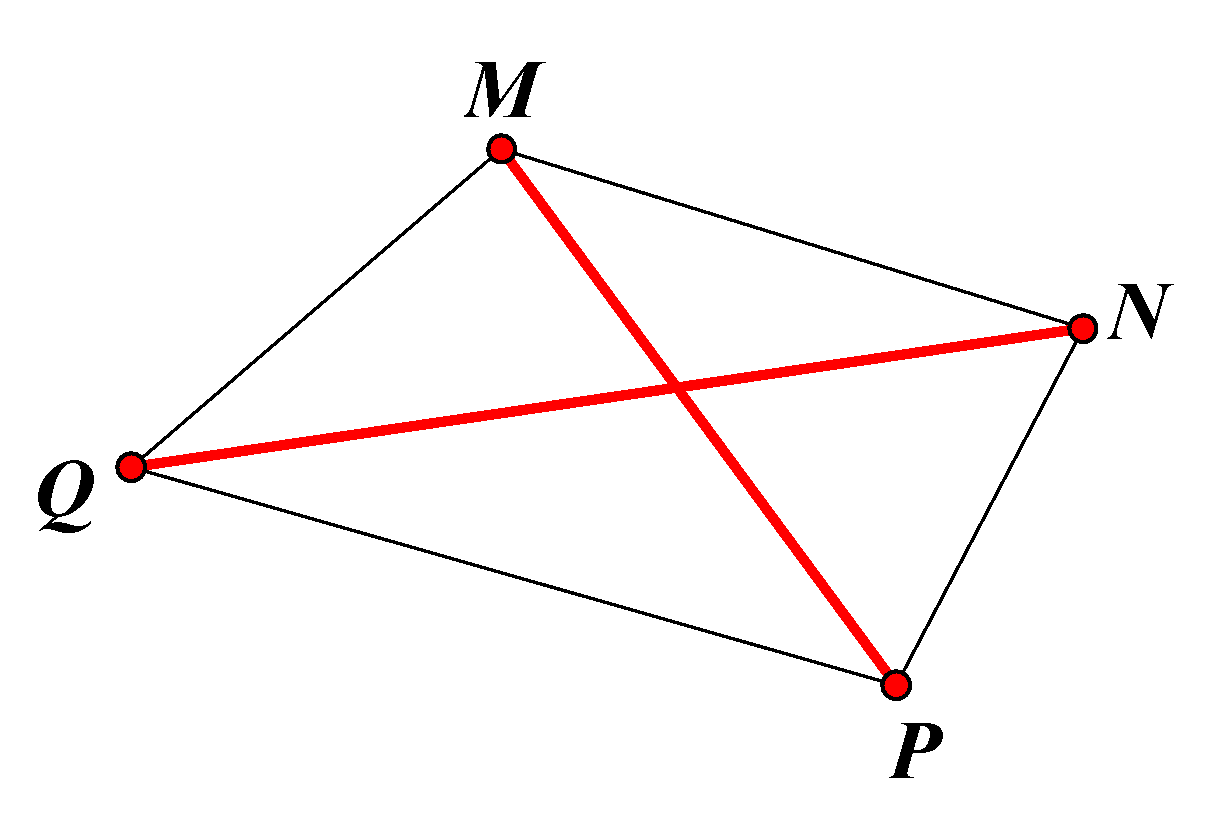
Trong tứ giác MNPQ có:

‒ Hai đỉnh đối nhau: M và P; N và Q;

‒ Hai đường chéo: MP và NQ;

‒ Hai cạnh đối nhau: MN và PQ; MQ và NP.

Vận dụng 1 (Trang 65):

Tìm các đỉnh, cạnh và đường chéo của tứ giác Long Xuyên CHRL (Hình 6).

Trả lời rút gọn:

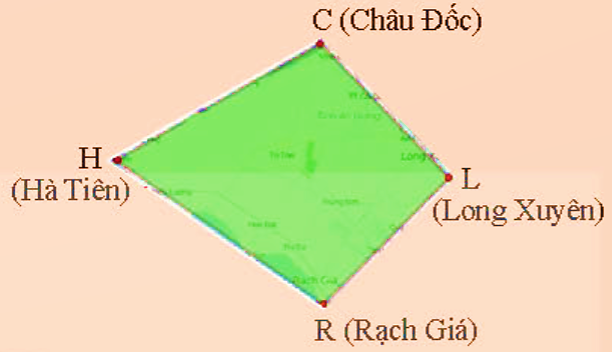
Trong tứ giác Long Xuyên CHRL có:

+ Các đỉnh: C, H, R, L;

+ Các cạnh: CH, HR, RL, LC;

+ Các đường chéo: CR và HL.

2. TỔNG CÁC GÓC CỦA MỘT TỨ GIÁC

Hoạt động 3 (Trang 65):

Đường chéo AC chia tứ giác ABCD thành hai tam giác ACB và ACD (Hình 7). Tính tổng các góc của tam giác ACB và tam giác ACD. Từ đó, ta có nhận xét gì về tổng các góc của tứ giác ABCD?

Trả lời rút gọn:

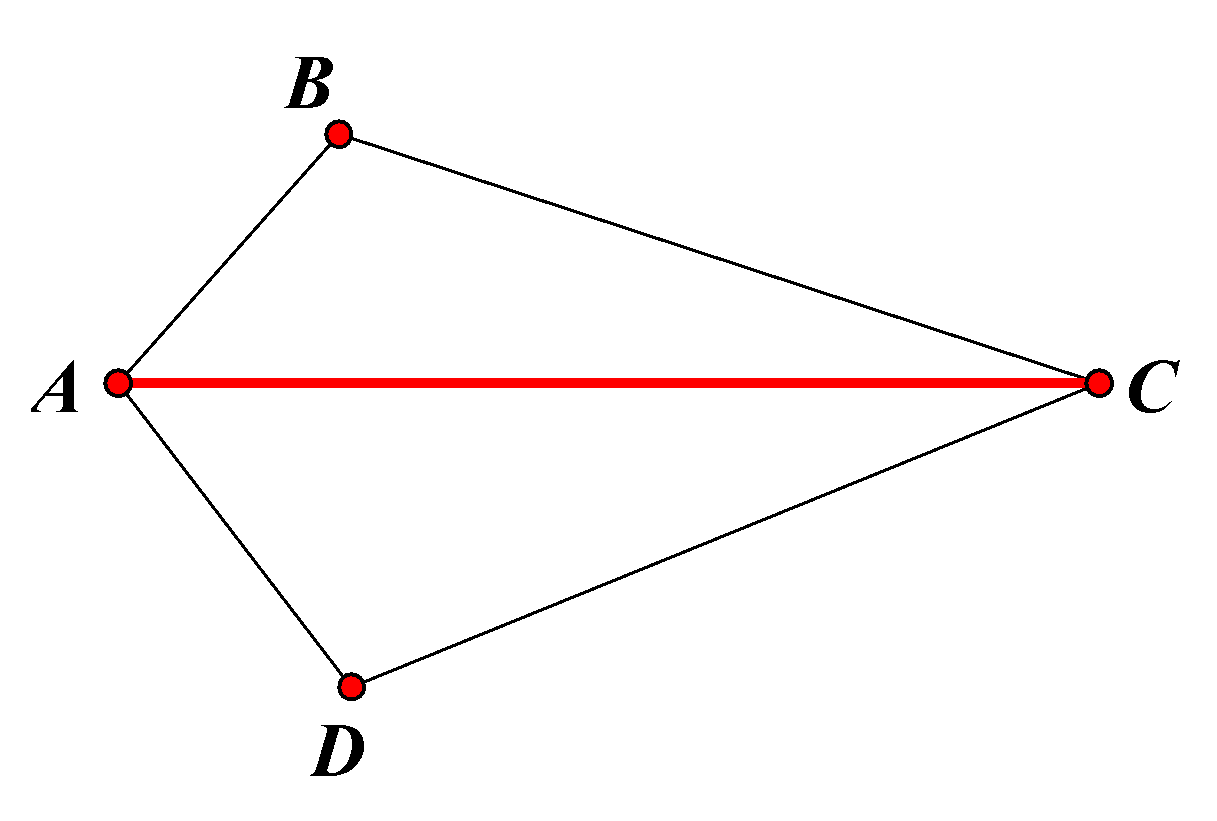
Xét tam giác ACB có:

(định lí tổng ba góc trong một tam giác).

Xét tam giác ACD có:

(định lí tổng ba góc trong một tam giác).

Do +

Suy ra

Hay

Vậy tổng các góc của tứ giác ABCD bằng

Thực hành 2 (Trang 66):

Tìm x trong mỗi tứ giác sau:

Trả lời rút gọn:

a) 

Xét tứ giác PQRS có: 

(định lí tổng các góc của một tứ giác)

Suy ra

Do đó

b) 

Xét tứ giác ABCD có: 

(định lí tổng các góc của một tứ giác)

Suy ra

c)

Xét tứ giác EFGH có: 

(định lí tổng các góc của một tứ giác)

Suy ra

Vận dụng 2 (Trang 66):

Phần thân của cái diều ở Hình 10a được vẽ lại như Hình 10b. Tìm số đo các góc chưa biết trong hình.

Trả lời rút gọn:

Xét và có:

AC là cạnh chung; 

AB = AD; 

BC = DC (gt).

Do đó = (c.c.c).

Suy ra (hai góc tương ứng).

Xét tứ giác ABCD có: 

(định lí tổng các góc của một tứ giác)

Suy ra

Hay

Do đó

Vậy

BÀI TẬP CUỐI SGK 

Bài tập 1 (Trang 66):

Tìm số đo các góc chưa biết của các tứ giác trong Hình 11.

Trả lời rút gọn:

a) Xét tứ giác ABCD có: 

(định lí tổng bốn góc của tứ giác)

Suy ra

b) Xét tứ giác MNPQ có: 

(định lí tổng bốn góc của tứ giác)

Suy ra

c) Có: (2 góc kề bù)

Xét tứ giác TSVU có: 

(định lí tổng bốn góc của tứ giác)

Suy ra

d) Xét tứ giác EFGH có: 

(định lí tổng bốn góc của tứ giác)

Suy ra

Bài tập 2 (Trang 66):

Góc kề bù với một góc của tứ giác được gọi là góc ngoài của tứ giác đó.

Hãy tính tổng số đo bốn góc ngoài  của tứ giác ABCD ở Hình 12.

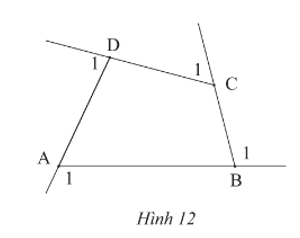
Trả lời rút gọn:

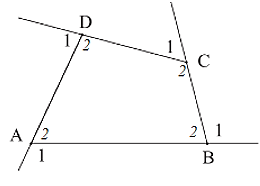
Xét tứ giác ABCD có:

  (định lí tổng các góc của một tứ giác)

Mặt khác: (hai góc kề bù)

Tương tự: ; ; .

Suy ra

Vậy tổng số đo bốn góc ngoài  của tứ giác ABCD bằng

Bài tập 3 (Trang 67):

Tứ giác ABCD có góc ngoài tại đỉnh B bằng 110°, Tính số đo góc D.

Trả lời rút gọn:

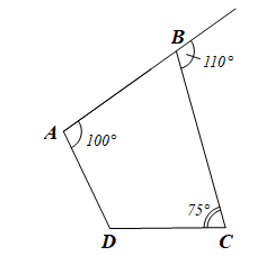
Do góc ngoài tại đỉnh B có số đo bằng 110° nên

Xét tứ giác ABCD có: 

(định lí tổng các góc của một tứ giác)

Suy ra

Do đó

Bài tập 4 (Trang 67):

Tứ giác ABCD có góc ngoài tại đỉnh A bằng 65°, góc ngoài tại đỉnh B bằng 100°, góc ngoài tại đỉnh C bằng 60°. Tính số đo góc ngoài tại đỉnh D.

Trả lời rút gọn:

Gọi lần lượt là các góc ngoài tại đỉnh A, đỉnh B, đỉnh C, đỉnh D (hình vẽ).

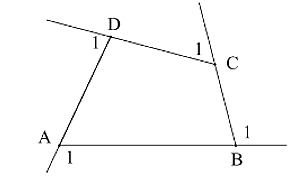
Xét tứ giác ABCD ta có: 

(ĐL tổng bốn góc trong tứ giác)

Suy ra

Bài tập 5 trang 67 sgk Toán 8 tập 1 CTST

Tứ giác ABCD có số đo . Tính số đo các góc của tứ giác đó.

Trả lời rút gọn:

Xét tứ giác ABCD có: 

(định lí tổng các góc của một tứ giác)

Suy ra

Hay

Bài tập 6 (Trang 67):

Ta gọi tứ giác ABCD với AB = AD, CB = CD (Hình 13) là hình “cái diều”.

a) Chứng minh rằng AC là đường trung trực của BD.

b) Cho biết .

Trả lời rút gọn:

a) Vì AB = AD nên A nằm trên đường trung trực của đoạn thẳng BD.

Vì CB = CD nên C nằm trên đường trung trực của đoạn thẳng BD.

Do đó AC là đường trung trực của đoạn thẳng BD.

b) Xét và có:

AC là cạnh chung; 

AB = AD; 

BC = DC (gt).

Do đó (c.c.c).

Suy ra (hai góc tương ứng).

Mà nên

Xét tứ giác ABCD có: 

(định lí tổng các góc của một tứ giác)

Suy ra

Do đó . Vậy và

Bài tập 7 (Trang 67):

Trên bản đồ, tứ giác BDNQ với các đỉnh là các thành phố Buôn Ma Thuột, Đà Lạt, Nha Trang, Quy Nhơn.

a) Tìm các cạnh kề và cạnh đối của cạnh BD.

b) Tìm các đường chéo của tứ giác.

Trả lời rút gọn:

a) Tứ giác BDNQ có:

+ Các cạnh kề: BD và BQ; DB và DN; ND và NQ; QN và QB;

+ Các cạnh đối: BD và NQ; DN và BQ.

b) Tứ giác BDNQ có các đường chéo BN và DQ.