Slide bài giảng toán 8 chân trời bài 3: Tính chất đường phân giác của tam giác

Tóm lược nội dung

BÀI 3. TÍNH CHẤT ĐƯỜNG PHÂN GIÁC CỦA TAM GIÁC

1. TÍNH CHẤT ĐƯỜNG PHÂN GIÁC CỦA TAM GIÁC

Hoạt động 1 (Trang 55): Cho tam giác ABC có đường phân giác AD. Vẽ đường thẳng qua B song song với AD và cắt đường thẳng AC tại E (Hình 1). Hãy giải thích tại sao:

a) tam giác BAE cân tại A

b)

Trả lời rút gọn:

a) Ta có: BE // AD suy ra (hai góc đồng vị), (hai góc so le trong)

AD là tia phân giác góc nên 

Do đó: => tam giác BAE cân tại A

b) Xét tam giác BCE có , theo định lí Thales ta có:  

Mà AE = AB (do tam giác ABE cân tại A)

Do đó:   

2. ÁP DỤNG TÍNH CHIA TỈ LỆ CỦA ĐƯỜNG PHÂN GIÁC CỦA TAM GIÁC

Thực hành (Trang 56): 

Tính độ dài cạnh MQ của tam giác MPQ trong Hình 6

Trả lời rút gọn:

Trong tam giác MPQ , ta có MN là đường phân giác góc M, suy ra nên =>

BÀI TẬP CUỐI SGK

Bài tập 1 (Trang 56): 

Tính độ dài x trong Hình 7

Trả lời rút gọn: 

a) Trong tam giác ABC , ta có: AD là đường phân giác góc A

suy ra ⬄ ⬄

b) Trong tam giác EFG , ta có EH là đường phân giác góc E,

 suy ra ⬄ ⬄ ⬄

c) Trong tam giác PQR , ta có: RS là đường phân giác góc R, 

suy ra ⬄ ⬄ x = 12

Bài tập 2 (Trang 57): 

Tam giác ABC có AB = 6cm, AC = 8 cm, BC = 10 cm. Đường phân giác của góc BAC cắt cạnh BC tại D

a) Tính độ dài các đoạn thẳng DB và DC

b) Tính tỉ số diện tích giữa ΔADB và ΔADC

Trả lời rút gọn:

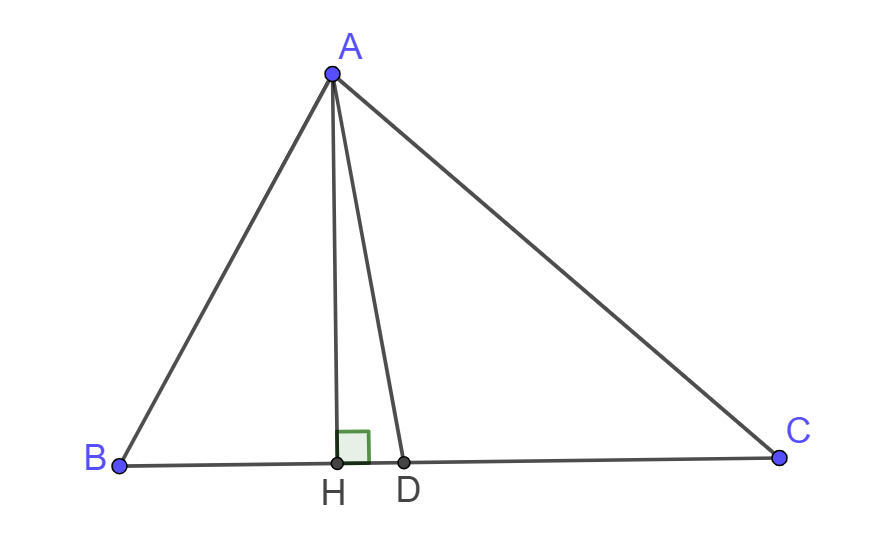
a) Tam giác ABC có AD là đường phân giác

Mà  

;  

b) Vẽ tại H

.

Bài tập 3 (Trang 56): 

Tam giác ABC có AB = 15cm, AC = 20 cm, BC = 25 cm. Đường phân giác của góc BAC cắt BC tại D. Qua D vẽ DE // AB (E∈AC)

a) Tính độ dài các đoạn thẳng DB, DC và DE

b) Chứng minh ABC là tam giác vuông. Tính diện tích tam giác ABC

c) Tính diện tích các tam giác ADB, ADE và DCE

Trả lời rút gọn:

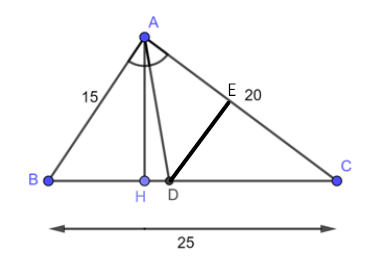
a) Trong tam giác ABC, ta có: AD là đường phân giác góc BAC

Suy ra: (tính chất đường phân giác)

Mà

Nên

Suy ra: (tính chất tỉ lệ thức)

Suy ra:

Nên:

Do đó, (cm)

Xét tam giác ABC có DE // AB, theo hệ quả định lí Thales ta có:

=> => .

b) Xét tam giác ABC ta có: AB = 15 cm, AC = 20 cm, BC = 25cm, nên 

suy ra tam giác ABC vuông tại A

c) Kẻ ta có:

Suy ra

.

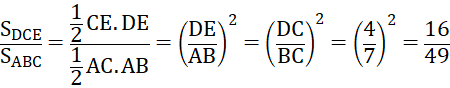
Bài tập 4 (Trang 57): 

Cho tam giác ABC vuông tại A có AB = 3 cm, AC = 4 cm. Đường phân giác của góc A cắt BC tại D.

a) Tính BC, DB, DC

b) Vẽ đường cao AH. Tính AH, HD và AD

Trả lời rút gọn:

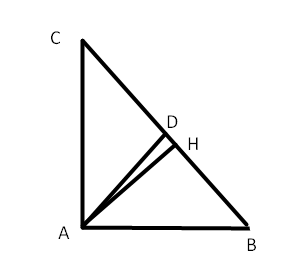
a) Tam giác ABC vuông tại A, áp dụng định lí Pythagore ta có:

  =>

AD là tia phân giác góc A nên

(cm)

b) Ta có:

(cm)

Tam giác ABH vuông tại H nên (cm)

Ta có: (cm)

Tam giác ADH vuông tại H nên:

  (cm)

Bài tập 5 (Trang 5): 

Cho tam giác ABC có trung tuyến AM. Đường phân giác của góc AMB cắt AB tại D và đường phân giác của góc AMC cắt AC tại E (Hình 8). Chứng minh DE // BC 

Trả lời rút gọn:

Xét tam giác ABM có MD là đường phân giác góc AMB suy ra

Xét tam giác ACM có ME là đường phân giác góc AMC suy ra  

Mà MB = MC, do đó: =, theo định lí Thales đảo ta có: DE // BC.