Slide bài giảng toán 8 chân trời bài tập cuối chương 1

Tóm lược nội dung

BÀI TẬP CUỐI CHƯƠNG 1

CÂU HỎI TRẮC NGHIỆM

Bài tập 1 trang 40 sgk Toán 8 tập 1 CTST

Biểu thức nào sau đây không phải đa thức?
A.

B.

C.

D. O

Trả lời rút gọn:

Đáp án C

Biểu thức trên không phải là đa thức vì có phép chia giữa hai biến x và z.

Bài tập 2 (Trang 40):

Đơn thức nào sau đây đồng dạng với đơn thức –2x³y?

A. x²yx.

B. 2x³yz.

C. –2x³z.

D. 3xy³.

Trả lời rút gọn:

Đáp án A

Có:

Do đó đơn thức trên đồng dạng với đơn thức

Bài tập 3 (Trang 40):

Biểu thức nào sau đây không phải là đa thức bậc 4?

A. 2x²yz.

B. x⁴ – x³y².

C. x²y + xyzt.

D. x⁴ – 2⁵.

Trả lời rút gọn:

Đáp án B

Hai hạng tử của đa thức x⁴ – x³y² có bậc lần lượt là 4 và 5 nên bậc của đa thức này bằng 5. Vậy biểu thức này không phải là đa thức bậc 4.

Bài tập 4 (Trang 40):

Biểu thức nào sau đây không phải là phân thức?
A.

B.

C.

D.

Trả lời rút gọn:

C

Biểu thức không phải là phân thức vì không phải là đa thức.

Bài tập 5 (Trang 40):

Kết quả của phép nhân (x + y – 1)(x + y + 1) là:

A. x² – 2xy + y² + 1.

B. x² + 2xy + y² – 1.

C. x² – 2xy + y² – 1.

D. x² + 2xy + y² + 1.

Trả lời rút gọn:

Đáp án B

M = (x+y-1).(x+y+1) = (x+y)² -1² = x²  + 2xy + y² - 1

Bài tập 6 (Trang 40):

Kết quả của phép nhân (2x + 1)(4x² – 2x + 1) là

Trả lời rút gọn:

Đáp án C

Có: N = (2x+1).(4x²-2x+1) = (2x+1).[(2x)² – 2x.1 + 1²]

= (2x)³ + 1³ =  8x³ + 1

Bài tập 7 (Trang 40):

Khi phân tích đa thức P = x⁴ – 4x² thành nhân tử thì được

A. P = x²(x – 2)(x + 2).

B. P = x(x – 2)(x + 2).

C. P = x²(x – 4)(x + 4).

D. P = x(x – 4)(x + 2).

Trả lời rút gọn:

A

P =  x⁴ – 4x² = (x²)² – (2x)² = (x² + 2x). (x² – 2x)

= x.(x+2).x.(-2) = x².(x - 2).(x + 2)

Bài tập 8 (Trang 40):

Kết quả của phép trừ

A.

B.

C.

D.

Trả lời rút gọn:

Đáp án B

=

=

=

=

Bài tập 9 (Trang 40):

Khi phân tích đa thức R = 4x² – 4xy + y² thành nhân tử thì được

A. R = (x + 2y)².

B. R = (x – 2y)².

C. R = (2x + y)².

D. R = (2x – y)².

Trả lời rút gọn:

Đáp án D

Ta có R = 4x² – 4xy + y² = (2x)² – 2.2x.y + y² = (2x – y)².

Bài tập 10 (Trang 40):

Khi phân tích đa thức S = x⁶ – 8 thành nhân tử thì được

A. S = (x² + 2)(x⁴ – 2x² + 4).

B. S = (x² – 2)(x⁴ – 2x² + 4).

C. S = (x² – 2)(x⁴ + 2x² + 4).

D. S = (x – 2)(x⁴ + 2x² + 4).

Trả lời rút gọn:

Đáp án C

Ta có: S = x⁶ – 8 = (x²)³ – 2³

 = (x² – 2)[(x²)² + x².2 + 2²]

BÀI TẬP TỰ LUẬN

Bài tập 11 (Trang 41):

Tính giá trị của đa thức P = xy²z – 2x²yz² + 3yz + 1 khi x = 1, y = –1, z = 2.

Trả lời rút gọn:

Thay x = 1, y = –1 và z = 2 vào đa thức P ta được:

P = 1.(–1)².2 – 2.1².(–1).2² + 3.(–1).2 + 1

   = 2 + 8 – 6 + 1

   = 5

Bài tập 12 (Trang 41):

Cho đa thức P = 3x²y – 2xy² – 4xy + 2. 

a) Tìm đa thức Q sao cho Q – P = –2x³y + 7x²y + 3xy.

b) Tìm đa thức M sao cho P + M = 3x²y² – 5x²y + 8xy.

Trả lời rút gọn:

a) Ta có: Q – P = –2x³y + 7x²y + 3xy.

Suy ra Q = P + (–2x³y + 7x²y + 3xy)

               = 3x²y – 2xy² – 4xy + 2 –2x³y + 7x²y + 3xy

               = –2x³y + (3x²y + 7x²y) – 2xy² + (– 4xy + 3xy) + 2 

               = –2x³y + 10x²y – 2xy² – xy + 2.

Vậy Q = – 2x³y +10x²y – 2xy² – xy + 2.

b) Ta có: P + M = 3x²y² – 5x²y + 8xy.

Suy ra M = 3x²y² – 5x²y + 8xy – P

                = 3x²y² – 5x²y + 8xy – (3x²y – 2xy² – 4xy + 2)

                = 3x²y² – 5x²y + 8xy – 3x²y + 2xy² + 4xy – 2

                = 3x²y² + (– 5x²y – 3x²y) + 2xy²  + (8xy + 4xy)– 2

                = 3x²y² –8x²y + 2xy² + 12xy– 2.

Vậy M = 3x²y² – 8x²y + 2xy² + 12xy – 2.

Bài tập 13 (Trang 41):

Thực hiện các phép tính sau:

a) x²y(5xy – 2x²y – y²);

b) (x – 2y)(2x² + 4xy).

Trả lời rút gọn:

a) x²y(5xy – 2x²y – y²)

= x²y.5xy – x²y.2x²y  – x²y.y²

= 5x³y² – 2x⁴y² – x²y³.

b) (x – 2y)(2x² + 4xy)

= x(2x² + 4xy) – 2y.(2x² + 4xy)

= 2x³ + 4x²y – 4x²y – 8xy²

= 2x³ – 8xy².

Bài tập 14 (Trang 41):

Thực hiện các phép tính sau:

a) 18x⁴y³ : 12(–x)³y

b)

Trả lời rút gọn: 

a) 18x⁴y³ : 12(–x)³y

= 18x⁴y³ : [12.(–x³)y]

= 18x⁴y³ : (–12.x³y)

= [18 : (–12)] . (x⁴ : x³) . (y³ : y)

=

b)

Bài tập 15 (Trang 41):

Tính:

a) (2x + 5)(2x – 5) – (2x + 3)(3x – 2);

b) (2x – 1)² – 4(x – 2)(x + 2).

Trả lời rút gọn:

a) (2x+5)(2x−5)−(2x+3)(3x−2)=4x²−25−6x²+4x−6x+6=−2x²−2x−19

b) (2x−1)²−4(x−2)(x+2)=4x²−4x+1−4x²+16=−4x+17

Bài tập 16 (Trang 41):

Phân tích các đa thức sau thành nhân tử.

a) (x – 1)² – 4;

b) 4x² + 12x + 9;

c) x³ – 8y⁶;

d) x⁵ – x³ – x² + 1;

e) –4x³ + 4x² + x – 1;

g) 8x³ + 12x² + 6x + 1.

Trả lời rút gọn:

a) (x – 1)² – 4

= (x – 1)² – 2²

= (x – 1 + 2)(x – 1 – 2)

= (x + 1)(x – 3).

b) 4x² + 12x + 9

= (2x²) + 2.2x.3 + 3²

= (2x + 3)².

c) x³ – 8y⁶

= x³ – (2y²)³

= (x – 2y²)[x² + x.2y² + (2y²)²]

= (x – 2y²)(x² + 2xy² + 4y⁴).

d) x⁵ – x³ – x² + 1

= (x⁵ – x³) – (x² – 1)

= x³(x² – 1) – (x² – 1)

= (x² – 1)(x³ – 1)

= (x + 1)(x – 1).(x – 1).(x² + x + 1)

= (x + 1)(x – 1)²(x² + x + 1).

e) –4x³ + 4x² + x – 1

= (–4x³ + 4x²) + (x – 1)

= –4x²(x – 1) + (x – 1)

= (x – 1)(–4x² + 1)

= (x – 1)[1² – (2x)²]

= (x – 1)(1 + 2x)(1 – 2x).

g) 8x³ + 12x² + 6x + 1

= (2x)³ + 3.(2x)².1 + 3.2x.1² + 1³

= (2x + 1)³.

Bài tập 17 (Trang 41):

Cho x + y = 3 và xy = 2. Tính x³ + y³.

Trả lời rút gọn:

x³+y³=(x+y)(x²−xy+y²)=(x+y)(x²+2xy+y²−3xy)=(x+y)[(x+y)²−3xy]

Thay x + y = 3 và xy = 2, ta có: 3×(3²−3×2)=9

Bài tập 18 (Trang 41):

Thực hiện các phép tính sau:

a)

b)

c)

d)

e)

g)

Trả lời rút gọn:

a)

b)

c)

d)

e)

g)

Bài tập 19 (Trang 41):

Thực hiện các phép tính sau:

a) b)

c)

d)

e)

g)

Trả lời rút gọn:

a) b)

c)

d)

e)

g)

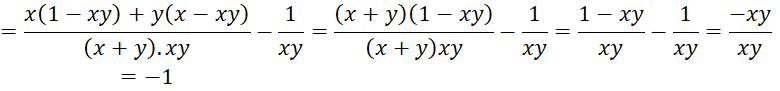
Bài tập 20 (Trang 41):

Hôm qua, thanh long được bán với giá a đồng mỗi kilôgam. Hôm nay, người ta đã giảm giá 1 000 đồng cho mỗi kilôgam thanh long. Với cùng số tiền b đồng thì hôm nay mua được nhiều hơn bao nhiêu kilôgam thanh long so với hôm qua?

Trả lời rút gọn:

+ Với số tiền b đồng, hôm qua sẽ mua được số kilogam thanh long (giá a đồng mỗi kilogam) là: (kg).

+ Hôm nay giá thanh long giảm 1 000 đồng cho mỗi kilogam nên giá thanh long hôm nay là a – 1 000 (đồng).

Khi đó với số tiền b đồng, hôm nay mua được số kilogam thanh long là: (kg).

+ Hôm nay mua được nhiều hơn hôm qua số kilogam thanh long là:

(kg)

Vậy hôm nay mua được nhiều hơn hôm qua kilogam thanh long.

Bài tập 21 (Trang 41):

Trên một dòng sông, một con thuyền đi xuôi dòng với tốc độ (x + 3) km/h và đi ngược dòng với tốc độ (x − 3) km/h (x > 3).

a) Xuất phát từ bến A, thuyền đi xuôi dòng trong 4 giờ, rồi đi ngược dòng trong 2 giờ. Tính quãng đường thuyền đã đi. Lúc này thuyền cách bến A bao xa?

b) Xuất phát từ bến A, thuyền đi xuôi dòng đến bến B cách bến A 15 km, nghỉ 30 phút, rồi quay về bến A. Sau bao lâu kể từ lúc xuất phát thì thuyền quay về đến bến A?

Trả lời rút gọn:

a) Thuyền đi xuôi dòng trong 4 giờ được quãng đường là: 4(x + 3) (km).

Thuyền đi ngược dòng trong 2 giờ được quãng đường là: 2(x – 3) (km).

Quãng đường thuyền đã đi là:

4(x + 3) + 2(x – 3) = 4x + 12 + 2x – 6 = 6x + 6 (km).

Lúc này thuyền cách bến A là:

4(x + 3) – 2(x – 3) = 4x + 12 – 2x + 6 = 2x + 18 (km).

b) Thời gian thuyền đi xuôi dòng từ A đến B là: (giờ).

Thời gian thuyền đi ngược dòng từ B về A là: (giờ).

Đổi 30 phút = 0,5 giờ.

Vậy thời gian kể từ khi thuyền xuất phát từ A đến B rồi quay về bến A là:

  (giờ)

Vậy sau giờ kể từ lúc xuất phát thì thuyền quay về đến bến A.