Slide bài giảng toán 8 chân trời bài 2: Đường trung bình của tam giác

Tóm lược nội dung

BÀI 2. ĐƯỜNG TRUNG BÌNH CỦA TAM GIÁC

1. ĐƯỜNG TRUNG BÌNH CỦA TAM GIÁC

Hoạt động 1 (Trang 52): 

Cho tam giác ABC, vẽ đường thẳng d đi qua trung điểm M của cạnh AB, song song với cạnh BC và cắt AC tại N (Hình 1). Hãy chứng minh N là trung điểm của AC

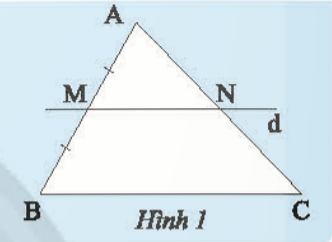
Trả lời rút gọn:

Xét tam giác ABC có MN // BC, theo định lí Thales ta có:

=> N là trung điểm của AC

Thực hành 1 (Trang 52):

Tìm độ dài đoạn thẳng NQ trong Hình 4

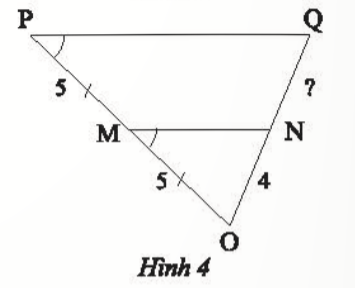
Trả lời rút gọn: 

Ta có: mà hai góc này ở vị trí đồng vị nên

Xét tam giác OPQ ta có: MN // PQ; M là trung điểm OP

⇒ MN là đường trung bình tam giác OPQ

⇒ N là trung điểm OQ 

⇒ NQ = ON = 4 

Vận dụng 1 (Trang 53):

Trong Hình 5, chứng minh MN là đường trung bình của tam giác ABC

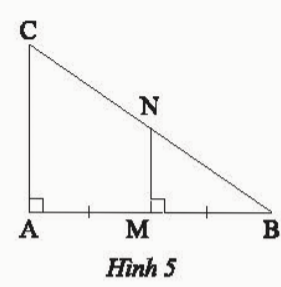
Trả lời rút gọn: 

Ta có: MN⊥AB,AC⊥AB nên MN // AC

Xét tam giác ABC có: MN // AC, M là trung điểm AB suy ra MN là đường trung bình tam giác ABC

2. TÍNH CHẤT CỦA ĐƯỜNG TRUNG BÌNH

Hoạt động 2 (Trang 53):

Cho M, N lần lượt là trung điểm của hai cạnh AB và AC của tam giác ABC.

a) Tính các tỉ số ;

b) Chứng minh MN // BC

c) Chứng minh

Trả lời rút gọn:

a) Vì M là trung điểm AB suy ra

Tương tự,

b) Xét tam giác ABC có:

Theo định lí Thales đảo ta có:

c) Xét tam giác ABC có MN // BC, 

Áp dụng hệ quả định lí Thales, ta có: 

Thực hành 2 (Trang 53):

Trong Hình 8, cho biết JK = 10 cm, DE = 6.5 cm, EL = 3.7 cm. Tính DJ, EF, DF, KL

Trả lời rút gọn: 

D là trung điểm của JK suy ra

E là trung điểm của JL suy ra JL = 2EL = 2 . 3,7 = 7,4 (cm)

Trong tam giác JKL có: D, E lần lượt là trung điểm của JK và JL

 suy ra DE là đường trung bình của tam giác JKL.

 suy ra KL = 2DE = 2 . 6,5 = 13 (cm)

Tương tự, ta có: EF là đường trung bình của tam giác JKL 

suy ra

DF là đường trung bình tam giác JKL suy ra DF= JL= x 7,4 = 3,7 (cm)

Vận dụng 2 (Trang 53):

Hãy tính khoảng cách BC trong phần HĐKĐ (trang 52)

Trả lời rút gọn: 

Xét tam giác ABC có: D, E là trung điểm của AB và AC 

nên DE là đường trung bình của tam giác ABC suy ra

Vậy BC = 2.DE = 90 (m)

BÀI TẬP CUỐI SGK

Bài tập 1 (Trang 53): 

Cho MN là đường trung bình của mỗi tam giác ABC trong Hình 9. Hãy tìm giá trị x trong mỗi hình

Trả lời rút gọn:

a) Xét tam giác ABC có MN là đường trung bình ta có: BC = 2 MN => x = 12

b) Xét tam giác ABC có MN là đường trung bình ta có: BC = 2MN => 2x + 3 = 14 suy ra x =

c) Xét tam giác ABC có MN là đường trung bình ta có: BC = 2MN suy ra 58=2(5x−1)⇒58=10x−2⇒x=6

Bài tập 2 (Trang 54): 

Tính độ dài đoạn PQ (hình 10)

Trả lời rút gọn:

Xét tam giác ABC có: 

AP = PB = 8cm; 

AQ = QC = 7 cm 

suy ra PQ là đường trung bình tam giác ABC 

nên

Bài tập 3 (Trang 54): 

Cho biết cạnh mỗi ô vuông bằng 1 cm. Tính độ dài các đoạn PQ, PR, RQ, AB, BC, CA trong Hình 11

Trả lời rút gọn:

Ta có:

Xét tam giác ABC có: P, Q lần lượt là trung điểm của BC và AC 

suy ra PQ là đường trung bình tam giác ABC 

nên

Tương tự:

Bài tập 4 (Trang 54): 

Cho hình thang ABCD (AB //CD) có E và F lần lượt là trung điểm hai cạnh bên AD và BC. Gọi K là giao điểm của AF và DC (Hình 12).

a) Tam giác FBA và tam giác FCK có bằng nhau không? Vì sao?

b) Chứng minh EF // CD // AB                     

c) Chứng minh

Trả lời rút gọn:

a) Xét tam giác FBA và FCK ta có:

(hai góc đối đỉnh)

FB = FC (gt)

(AB // CD, hai góc so le trong)

Suy ra (g.c.g)

b) suy ra FA = FK

Xét tam giác ADK có: EA = ED, FA = FK, 

suy ra EF là đường trung bình tam giác ABC 

nên

Mà suy ra

c) EF là đường trung bình tam giác ADK suy ra

Mà CK = BA (do ) nên

Bài tập 5 (Trang 54): 

Cho tam giác ABC nhọn. Gọi M, N, P lần lượt là trung điểm của AB, AC, BC. Kẻ đường cao AH. Chứng minh rằng tứ giác MNPH là hình thang cân.

Trả lời rút gọn:

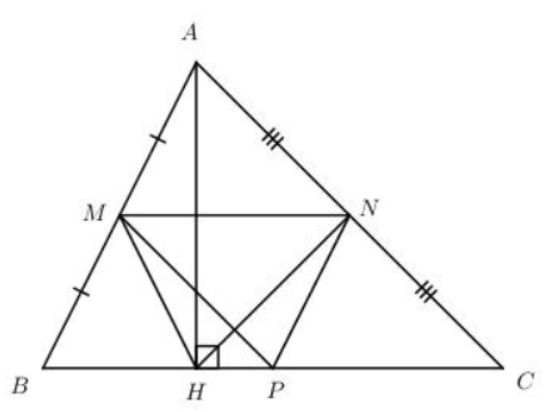
Xét tam giác ABC ta có:

M là trung điểm của AB (gt) ;

N là trung điểm của AC (gt) ;

⇒ MN là đường trung bình của tam giác ABC ⇒MN//BC

⇒ Tứ giác MNPH là hình thang.

Xét tam giác ABC ta có 

M là trung điểm của AB (gt) ;

P là trung điểm của BC

⇒MP là đường trung bình của tam giác ABC ⇒MP= AC

ΔACH vuông tại H có HN là trung tuyến (N là trung điểm của AC)⇒NH= AC. Mà MP= AC(cmt)

⇒NH=MP

Hình thang MNPH (MN//PH) có MP=NH nên là hình thang cân.

Bài tập 6 (Trang 54): 

Một mái nhà được vẽ lại như Hình 13. Tính độ dài x trong hình mái nhà.

Trả lời rút gọn:

Xét tam giác ABH có: AD = BD, BE = EH suy ra DE là đường trung bình tam giác ABH nên DE= AH⇒x= .2,8=1,4 (m)

Bài tập 7 (Trang 54): 

Ảnh chụp từ Google Maps của một trường học được cho trong Hình 14. Hãy tính chiều dài cạnh DE, cho biết BC = 232 m và B, C lần lượt là trung điểm AD và AE

Trả lời rút gọn:

Xét tam giác ADE có: B, C lần lượt là trung điểm AD và AE nên BC là đường trung bình của tam giác ADE suy ra DE=2BC=2.232=464 (m)