Slide bài giảng toán 8 chân trời bài 3: Hằng đẳng thức đáng nhớ

Tóm lược nội dung

BÀI 3. HẰNG ĐẲNG THỨC ĐÁNG NHỚ

1. BÌNH PHƯƠNG CỦA MỘT TỔNG, MỘT HIỆU

Hoạt động 1 trang 18 sgk Toán 8 tập 1 CTST

a) Ba bạn An, Mai và Bình viết biểu thức biểu thị tổng diện tích S của các phần tô màu trong Hình 1 như sau:

An: S = (a + b)².

Mai: S = a² + b² + ab + ba.

Bình: S = a² + 2ab + b².

Kết quả của mỗi bạn có đúng không? Giải thích.

b) Thực hiện phép nhân và rút gọn đa thức của bạn An.

c) Bằng cách làm tương tự ở câu b), có thể biến đổi biểu thức (a − b)² thành biểu thức nào?

Trả lời rút gọn: 

a) Ta xét các cách tính diện tích của các phần tô màu trong Hình 1 như sau:

Cách 1: Tính diện tích của hình vuông được ghép bởi 4 hình:

+ Cạnh của hình vuông ABCD được tạo thành là: a + b.

+ Diện tích S của các phần tô màu chính là diện tích của hình vuông ABCD, và bằng:

S = (a + b)² .

Do đó kết quả của bạn An là đúng.

Cách 2: Tính diện tích mỗi hình:

+ Diện tích hình vuông màu vàng AEHG là: a².

+ Diện tích hình vuông màu xanh HICK là: b².

+ Diện tích hình chữ nhật màu hồng EBIH là: ab.

+ Diện tích hình chữ nhật màu hồng GHKD là: ba.

+ Diện tích S của các phần tô màu là: 

a² + b² + ab + ba.

Do đó kết quả của bạn Mai là đúng.

Cách 3: Tính tổng diện tích hai hình chữ nhật ABIG và GICD (hình vẽ dưới đây).

+ Diện tích hình chữ nhật ABIG là: 

a.(a + b) = a.a + a.b = a² + ab.

+ Diện tích hình chữ nhật GICD là: 

(a + b).b = a.b + b.b = ab + b².

+ Diện tích S của các phần tô màu là: 

a² + ab + ab + b² = a² + 2ab + b².

Vậy kết quả của bạn Bình là đúng.

Thực hành 1 (Trang 19):

Viết các biểu thức sau thành đa thức:

a) (3x + 1)²

b) (4x + 5y)²

c)

d) (–x + 2y²)²

Trả lời rút gọn:

a) (3x + 1)²

= (3x)² + 2.3x.1 + 1²

= 9x² + 6x + 1.

b) (4x + 5y)²

= (4x)² + 2.4x.5y + (5y)²

= 16x² + 40xy + 25y².

c)

d) (–x + 2y²)²

= (–x)² + 2.(–x).2y² + (2y²)²

= x² – 4xy² + 4y⁴.

Thực hành 2 (Trang 19):

Viết các biểu thức sau thành bình phương của một tổng hoặc một hiệu:

a) a² + 10ab + 25b²

b) 1 + 9a² – 6a

Trả lời rút gọn:

a) a² + 10ab + 25b²

= a² + 2.a.5b + (5b)²

= (a + 5b)².

b) 1 + 9a² – 6a

= 1 – 6a + 9a²

= 1² – 2.1.3a + (3a)²

= (1 – 3a)².

Hoặc ta có thể viết như sau:

1 + 9a² – 6a

= 9a² – 6a + 1

= (3a)² – 2.3a.1 + 1²

= (3a – 1)².

Thực hành 3 (Trang 19):

Tính nhanh:

a) 52² 

b) 98² 

Trả lời rút gọn:

a) 52² = (50 + 2)² = 50² + 2.50.2 + 2² 

= 2 500 + 200 + 4 = 2 704.

b) 98² = (100 – 2)² = 100² – 2.100.2 + 2² 

= 10 000 – 400 + 4 = 9 604.

Vận dụng 1 (Trang 19):

a) Một mảnh vườn hình vuông có cạnh 10 m được mở rộng cả hai cạnh thêm x (m) như Hình 2a. Viết biểu thức (dạng đa thức thu gọn) biểu thị diện tích mảnh vườn sau khi mở rộng.

b) Một mảnh vườn hình vuông sau khi mở rộng mỗi cạnh 5 m thì được một mảnh vườn hình vuông với cạnh là x (m) như Hình 2b. Viết biểu thức (dạng đa thức thu gọn) biểu thị diện tích mảnh vườn trước khi mở rộng.

Trả lời rút gọn:

a) Mảnh vườn hình vuông có cạnh 10 m được mở rộng cả hai cạnh thêm x (m) nên mảnh vườn lúc này có dạng hình vuông với độ dài cạnh là 10 + x (m).

Diện tích mảnh vườn sau khi mở rộng là:

(10 + x)² = 10² + 2.10.x + x² 

= 100 + 20x + x² (m²).

Vậy biểu thức biểu thị diện tích mảnh vườn sau khi mở rộng là 100 + 20x + x² (m²).

b) Mảnh vườn hình vuông trước khi mở rộng có độ dài cạnh là: x – 5 (m).

Diện tích mảnh vườn hình vuông trước khi mở rộng là:

(x – 5)² = x² – 2.x.5 + 5² = x² – 10x + 25 (m²).

Vậy biểu thức biểu thị diện tích mảnh vườn trước khi mở rộng là x² – 10x + 25 (m²).

2. HIỆU CỦA HAI BÌNH PHƯƠNG

Hoạt động 2 (Trang 20):

a) Từ Hình 3a, người ta cắt ghép tạo thành Hình 3b. Viết hai biểu thức khác nhau, mỗi biểu thức biểu thị diện tích (phần tô màu) của một trong hai hình bên.

b) Thực hiện phép nhân và rút gọn đa thức, biến đổi biểu thức (a + b)(a – b) thành một đa thức thu gọn. Từ đó, có kết luận gì về diện tích của hai hình bên?

Trả lời rút gọn: 

+ Diện tích hình vuông ABCD là: a².

+ Diện tích hình vuông EGHD là: b².

+ Diện tích phần tô màu ở Hình 3a là: a² – b².

+ Chiều dài của hình chữ nhật trong Hình 3b là: a + b.

+ Chiều rộng của hình chữ nhật trong Hình 3b là: a – b.

+ Diện tích hình chữ nhật (phần tô màu) trong Hình 3b là: (a + b)(a – b).

b) Ta có:

(a + b)(a – b) = a.(a – b) + b.(a – b) = a.a – ab + ba – b.b = a² – b².

Vậy hai hình trên có diện tích bằng nhau.

Thực hành 4 (Trang 20):

Thực hiện các phép nhân:

a) (4 – x).(4 + x) 

b) (2y + 7z).(2y – 7z) 

c) (x + 2y²).(x – 2y²) 

Trả lời rút gọn:

a) (4 – x).(4 + x) = 4² – x² = 16 – x².

b) (2y + 7z).(2y – 7z) = (2y)² – (7z)² = 4y² – 49z².

c) (x + 2y²).(x – 2y²) = x² – (2y²)² = x² – 4y⁴.

Thực hành 5 (Trang 20):

Tính nhanh:

a) 82 . 78 

b) 87 . 93 

c) 125² – 25²

Trả lời rút gọn:

a) 82 . 78 = (80 + 2).(80 – 2) = 80² – 2² = 6 400 – 4 = 6 396.

b) 87 . 93 = (90 – 3).(90 + 3) = 90² – 3² = 8 100 – 9 = 8 091.

c) 125² – 25² = (125 + 25).(125 – 25) = 150 . 100 = 15 000.

Vận dụng 2 (Trang 20):

Giải đáp câu hỏi ở trang 18

Trả lời rút gọn:

65² – 35² = (65 + 35) . (65 – 35) = 100 . 30 = 3 000.

102 . 98 = (100 + 2) . (100 – 2) = 100² – 2² = 10 000 – 4 = 9 996.

3. LẬP PHƯƠNG CỦA MỘT TỔNG, MỘT HIỆU

Hoạt động 3 trang 20 sgk Toán 8 tập 1 CTST

Hoàn thành các phép nhân đa thức sau vào vở, thu gọn kết quả nhận được: 

(a + b)³ = (a + b)(a + b)²

             = (a + b)(…)

             = …

(a – b)³ = (a – b)(a – b)²

             = (a – b)(…)

             = …

Trả lời rút gọn:

(a + b)³ = (a + b)(a + b)²

= (a + b)(a² + 2ab + b²)

= a(a² + 2ab + b²) + b(a² + 2ab + b²)

= a.a² + a.2ab + a.b² + b.a² + b.2ab + b.b²

= a³ + 2a²b + ab² + a²b + 2ab² + b³

= a³ + (2a²b + a²b) + (ab² + 2ab²) + b³

= a³ + 3a²b + 3ab² + b³.

(a – b)³ = (a – b)(a – b)²

 = (a – b)(a² – 2ab + b²)

= a(a² – 2ab + b²) – b(a² – 2ab + b²)

= a.a² – a.2ab + a.b² – b.a² + b.2ab – b.b²

= a³ – 2a²b + ab² – a²b + 2ab² – b³

= a³ – (2a²b + a²b) + (ab² + 2ab²) – b³

= a³ – 3a²b + 3ab² – b³.

Thực hành 6 (Trang 21):

Tính:

a) (x + 2y)³

b) (3y – 1)³

Trả lời rút gọn:

a) (x + 2y)³

= x³ + 3.x².2y + 3.x.(2y)² + (2y)³

= x³ + 6x²y + 12xy² + 8y³.

b) (3y – 1)³

= (3y)³ – 3.(3y)².1 + 3.3y.1² – 1³

= 27y³ – 27y² + 9y – 1.

Vận dụng 3 (Trang 21):

Một thùng chứa dạng hình lập phương có độ dài cạnh bằng x (cm). Phần vỏ bao gồm nắp có độ dày 3 cm. Tính dung tích (sức chứa) của thùng, viết kết quả dưới dạng đa thức.

Trả lời rút gọn:

Phần lòng trong của thùng chứa có dạng hình lập phương với độ dài cạnh là:

x – 3 – 3 = x – 6 (cm).

Thể tích phần lòng trong của thùng là:

(x – 6)³ = x³ – 3.x².6 + 3.x.6² – 6³

= x³ – 18x² + 108x – 216 (cm³).

Vậy dung tích (sức chứa) của thùng là x³ – 18x² + 108x – 216 (cm³).

4. TỔNG VÀ HIỆU CỦA HAI LẬP PHƯƠNG

Hoạt động 4 (Trang 21):

Sử dụng quy tắc chuyển vế và các tính chất của phép toán, hoàn thành các biến đổi sau vào vở:

(a + b)³ = a³ + 3a²b + 3ab² + b³

a³ + b³ = (a + b)³ – 3a²b – 3ab²

           = (a + b)³ – 3ab(a + b)

           = (a + b)(…)

           = …

(a – b)³ = a³ – 3a²b + 3ab² – b³

a³ – b³ = (a – b)³ + 3a²b – 3ab²

           = (a – b)³ + 3ab(a – b)

           = (a – b)(…)

           = …

Trả lời rút gọn: 

(a + b)³ = a³ + 3a²b + 3ab² + b³

a³ + b³ = (a + b)³ – 3a²b – 3ab²

           = (a + b)³ – 3ab(a + b)

           = (a + b)[(a + b)² – 3ab]

           = (a + b)(a² + 2ab + b² – 3ab)

           = (a + b)(a² – ab + b²).

(a – b)³ = a³ – 3a²b + 3ab² – b³

a³ – b³ = (a – b)³ + 3a²b – 3ab²

           = (a – b)³ + 3ab(a – b)

           = (a – b)[(a – b)² + 3ab]

           = (a – b)(a² – 2ab + b² + 3ab)

           = (a – b)(a² + ab + b²).

Thực hành 7 (Trang 21):

Viết các đa thức sau dưới dạng tích:

a) 8y³ + 1 

b) y³ – 8 

Trả lời rút gọn:

a) 8y³ + 1 = (2y)³ + 1

                = (2y + 1)[(2y)² – 2y.1 + 1²]

                = (2y + 1)(4y² – 2y + 1)

b) y³ – 8 = y³ – 2³

              = (y – 2)(y² + y.2 + 2²)

              = (y – 2)(y² + 2y + 4).

Thực hành 8 (Trang 21):

Tính:

a) (x + 1)(x² – x + 1)

b)

Trả lời rút gọn:

a) (x + 1)(x² – x + 1)

= x³ + 1³

= x³ + 1.

b)

Vận dụng 4 (Trang 22):

Từ một khối lập phương có cạnh bằng 2x + 1, ta cắt bỏ một khối lập phương có cạnh bằng x + 1 (xem Hình 5). Tính thể tích phần còn lại, viết kết quả dưới dạng đa thức.

Trả lời rút gọn:

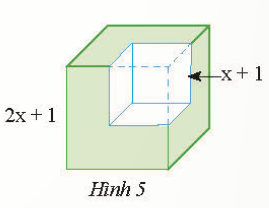
Thể tích của khối lập phương có cạnh bằng 2x + 1 là: (2x + 1)³.

Thể tích của khối lập phương có cạnh bằng x + 1 là: (x + 1)³.

Cách 1: Thể tích phần còn lại là:

(2x + 1)³ – (x + 1)³

= (2x)³ + 3.(2x)².1 + 3.2x.1² + 1³ – (x³ + 3.x².1 + 3.x.1² + 1³)

= 8x³ + 12x² + 6x + 1 – x³ – 3x² – 3x – 1

= (8x³ –  x³) + (12x² – 3x²) + (6x – 3x) + (1 – 1)

= 7x³ + 9x² + 3x.

Cách 2: Thể tích phần còn lại là:

(2x + 1)³ – (x + 1)³

= [(2x + 1) – (x + 1)].[(2x + 1)² + (2x + 1).(x + 1) + (x + 1)²]

= [2x + 1 – x – 1].[(2x)² + 2.2x.1 + 1² + (2x.x + 2x.x + 1.x + 1.1) + x² + 2.x.1 + 1²]

= x.[4x² + 4x + 1 + 2x² + 3x + 1 + x² + 2x + 1]

= x.[(4x² + 2x² + x²) + (4x + 3x + 2x) + (1 + 1 + 1)]

= x.[7x² + 9x + 3]

= 7x³ + 9x² + 3x.

BÀI TẬP CUỐI SGK  

Bài tập 1 (Trang 22):

Tính:

a) (3x + 4)²;

b) (5x – y)²;

c)

Trả lời rút gọn:

a) (3x + 4)²

= (3x)² + 2.3x.4 + 4²

= 9x² + 24x + 16.

b) (5x – y)²

= (5x)² – 2.5x.y + y²

= 25x² – 10xy + y².

c)

Bài tập 2 (Trang 22):

Viết các biểu thức sau thành bình phương của một tổng hoặc một hiệu:

a) x² + 2x + 1

b) 9 – 24x + 16x²

c)

Trả lời rút gọn:

a) x² + 2x + 1

= x² + 2.x.1 + 1²

= (x + 1)².

b) 9 – 24x + 16x²

= 3² – 2.3.4x + (4x)²

= (3 – 4x)².

Ta cũng có thể viết như sau:

9 – 24x + 16x²

= 16x² – 24x + 9

= (4x)² – 2.4x.3 + 3²

= (4x – 3)².

c)

=

=

=

Bài tập 3 (Trang 22):

Viết các biểu thức sau thành đa thức:

a) (3x – 5)(3x + 5);

b) (x – 2y)(x + 2y);

c)

Trả lời rút gọn:

a) (3x – 5)(3x + 5)

= (3x)² – 5²

= 9x² – 25.

b) (x – 2y)(x + 2y)

= x² – (2y)²

= x² – 4y².

c)

Bài tập 4 (Trang 22):

a) Viết biểu thức tính diện tích của hình vuông có cạnh bằng 2x + 3 dưới dạng đa thức.

b) Viết biểu thức tính thể tích của khối lập phương có cạnh bằng 3x − 2 dưới dạng đa thức.

Trả lời rút gọn:

a) Biểu thức tính diện tích của hình vuông có cạnh bằng 2x + 3 là:

(2x + 3)² = (2x)² + 2.2x.3 + 3² = 4x² + 12x + 9.

b) Biểu thức tính thể tích của khối lập phương có cạnh bằng 3x − 2 là:

(3x – 2)³ = (3x)³ – 3.(3x)².2 + 3.3x.2² – 2³

= 27x³ – 54x² + 36x – 8.

Bài tập 5 (Trang 22):

Tính nhanh:

a) 38 . 42

b) 102² 

Trả lời rút gọn:

a) 38 . 42 = (40 – 2).(40 + 2) = 40² – 2² = 1 600 – 4 = 1 596.

b) 102² = (100 + 2)² = 100² + 2.100.2 + 2² = 10 000 + 400 + 4 = 10 404.

Bài tập 6 (Trang 22):

Viết các biểu thức sau thành đa thức:

a) (2x – 3)³;

b) (a + 3b)³;

c) (xy –1)³.

Trả lời rút gọn:

a) (2x – 3)³

= (2x)³ – 3.(2x)².3 + 3.2x.3² – 3³

= 8x³ – 36x² + 54x – 8.

b) (a + 3b)³

= a³ + 3.a².3b + 3.a.(3b)² + (3b)³

= a³ + 9a²b + 27ab² + 27b³.

c) (xy –1)³

= (xy)³ – 3.(xy)².1 + 3.xy.1² – 1³

= x³y³ – 3x²y² + 3xy – 1.

Bài tập 7 (Trang 22):

Viết các biểu thức sau thành đa thức:

a) (a – 5)(a² + 5a + 25);

b) (x + 2y)(x² – 2xy + 4y²).

Trả lời rút gọn:

a) (a – 5)(a² + 5a + 25)

= (a – 5)(a² + a.5 + 5²)

= a³ – 5³

= a³ – 125.

b) (x + 2y)(x² – 2xy + 4y²)

= (x + 2y).[x² – x.2y + (2y)²]

= x³ + (2y)³

= x³ + 8y³.

Bài tập 8 (Trang 22):

Viết các biểu thức sau thành đa thức:

a) (a – 1)(a + 1)(a² + 1);

b) (xy + 1)² – (xy – 1)².

Trả lời rút gọn:

a) (a – 1)(a + 1)(a² + 1)

= (a² – 1)(a² + 1)

= (a²)² – 1²

= a⁴ – 1.

b) (xy + 1)² – (xy – 1)²

= [(xy + 1) + (xy – 1)].[(xy + 1) – (xy – 1)]

= [xy + 1 + xy – 1].[xy + 1 – xy + 1]

= 2xy.2

= 4xy.

Bài tập 9 (Trang 22):

a) Cho x + y = 12 và xy = 35. Tính (x − y)².

b) Cho x – y = 8 và xy = 20. Tính (x + y)².

c) Cho x + y = 5 và xy = 6. Tính x³ + y³.

d) Cho x – y = 3 và xy = 40. Tính x³ – y³.

Trả lời rút gọn:

a) Ta có: (x − y)² = x² – 2xy + y²

= x² + 2xy + y² – 4xy

= (x + y)² – 4xy

Thay x + y = 12 và xy = 35 vào biểu thức trên ta có:

(x − y)² = (x + y)² – 4xy = 12² – 4.35 = 144 – 140 = 4.

b) Ta có: (x + y)² = x² + 2xy + y²

= x² – 2xy + y² + 4xy

= (x – y)² + 4xy

Thay x – y = 8 và xy = 20 vào biểu thức trên ta có:

(x + y)² = (x – y)² + 4xy = 8² + 4.20 = 64 + 80 = 144.

c) Ta có: x³ + y³ = (x + y).(x² – xy + y²)

= (x + y).(x² + 2xy + y² – 3xy)

= (x + y).[(x + y)² – 3xy]

= (x + y)³ – 3xy.(x+y)

Thay x + y = 5 và xy = 6 vào biểu thức trên ta có:

x³ + y³ = (x + y)³ – 3xy.(x+y) = 5³ – 3.6.5 = 35.

d) Ta có: x³ – y³ = (x – y).(x² + xy + y²)

= (x – y).(x² – 2xy + y² + 3xy)

= (x – y).[(x – y)² + 3xy]

= (x – y)³ + 3xy. (x – y)

Thay x – y = 3 và xy = 40 vào biểu thức trên ta có:

x³ – y³ = (x – y)³ + 3xy. (x – y) =  3³ + 3.40.3 = 387.

Bài tập 10 (Trang 22):

Cho hình hộp chữ nhật có chiều dài, chiều rộng, chiều cao đều bằng 5 cm. Thể tích của hình hộp chữ nhật sẽ tăng bao nhiêu nếu:

a) Chiều dài và chiều rộng tăng thêm a cm?

b) Chiều dài, chiều rộng, chiều cao đều tăng thêm a cm?

Trả lời rút gọn:

Thể tích hình hộp chữ nhật có chiều dài, chiều rộng, chiều cao đều bằng 5 cm là:

5³ = 125 (cm³)

a) Chiều dài của hình hộp chữ nhật sau khi tăng thêm a cm là: 5 + a (cm).

Chiều rộng của hình hộp chữ nhật sau khi tăng thêm a cm là: 5 + a (cm).

Thể tích hình hộp chữ nhật lúc sau là:

(5 + a).(5 + a).5 = (5 + a)².5

                          = (5² + 2.5.a + a²).5

= (25 + 10a + a²).5

= 25.5 + 10a.5 + a².5

= 125 + 50a + 5a² (cm³).

Khi đó thể tích của hình hộp chữ nhật đã tăng thêm là:

125 + 50a + 5a² – 125 = 5a² + 50a (cm³).

b) Chiều cao của hình hộp chữ nhật sau khi tăng thêm a cm là: 5 + a (cm).

Thể tích hình hộp chữ nhật lúc sau là:

(5 + a).(5 + a).(5 + a) = (5 + a)³

= 5³ + 3.5².a + 3.5.a² + a³

= 125 + 75a + 15a² + a³ (cm³).

Khi đó thể tích của hình hộp chữ nhật đã tăng thêm là:

125 + 75a + 15a² + a³ – 125 = a³ + 15a² + 75a (cm³).