Dạng bài tập Xác định độ dịch chuyển, quãng đường đi được, tốc độ và vận tốc

Bài tập 1:

a) Quãng đường đi được trong cả chuyến đi là:

$S=S_{1}+S_{2}=6+20=26 km$

b) Độ dịch chuyển tổng hợp của người đó là:

$d=\sqrt{d_{1}^{2}+d_{2}^{2}}=\sqrt{6^{2}+20^{2}}=20,88 km$

Bài tập 2:

a) Các vectơ dịch chuyển:

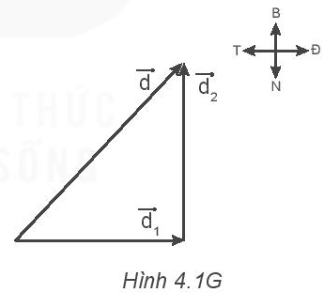
b) Độ dịch chuyển tổng hợp: 

$d=\sqrt{d_{1}^{2}+d_{2}^{2}}=\sqrt{3^{2}+4^{2}}=5m$

Ta có: $tan\alpha=\frac{d_{2}}{d_{1}}=\frac{4}{3}=53^{\circ}$

Vậy độ dịch chuyển d = 5 m, theo hướng đông - bắc $53^{\circ}$

Bài tập 3:

Cách 1:

Trong thời gian $(t_{1}+t_{2})$ con tàu đã lặn sâu được một đoạn $d=v(t_{1}+t_{2})\Rightarrow v=\frac{d}{t_{1}+t_{2}}$ (1)

Trong thời gian t₁ tín hiệu phát truyền được một đoạn $d_{2}=ut_{2}$

Vì $d=d_{1}+d_{2}=u(t_{1}+t_{2})$ (2)

Từ (1) và (2) ⇒ $v=u \frac{t_{1}-t_{2}}{t_{1}+t_{2}}$

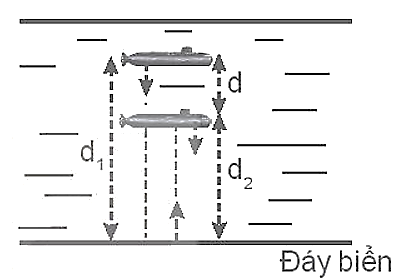
Cách 2:

Độ dịch chuyển của tàu ngầm từ khi phát tín hiệu âm tới khi nhận được tín hiệu là:

$\vec{d}=\vec{v}(t_{1}+t_{2}) \Rightarrow v=\frac{d}{t_{1}+t_{2}}$ (1)

Độ dịch chuyển của tín hiệu âm từ khi được phát ra từ tàu tới khi phản hồi về tàu là $\vec{d}=\vec{d}_{1}+\vec{d}_{2}$ trong đó $\vec{d}_{1}$ là độ dịch chuyển của tín hiệu phát: $\vec{d}_{1}=\vec{u}.t_{1};\vec{d}_{2}$ là độ dịch chuyển của tín hiệu phản hồi: $\vec{d}_{2}=\vec{u}.t_{2}$ (dấu “- ” vì tín hiệu phản hồi chuyển động ngược chiều với tín hiệu phát).

$d'=ut_{1}-ut_{2}\Rightarrow d'=u(t_{1}-t_{2})$

Hình trên cho thấy $\vec{d'}=\vec{d} \Rightarrow d=u(t_{1}-t_{2})$ (2)

Từ (1) và (2) ⇒ $v=u \frac{t_{1}-t_{2}}{t_{1}+t_{2}}$