Bài tập dạng quan hệ giữa các yếu tố trong tam giác

Bài tập 1: Xét $\Delta ABC$ có: $\hat{A}+\hat{B}+\hat{C}=180^{o}$

Nên $\hat{C}=180^{o}-\hat{A}-\hat{B}=180^{o}-40^{o}-95^{o}=45^{o}$

Ta có: $\hat{A} < \hat{C} < \hat{B}$ nên BC < AB < AC

Bài tập 2: 

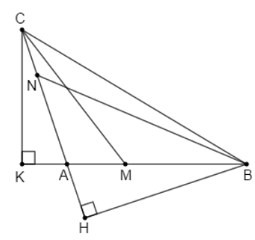
Từ B kẻ BH vuông góc với AC, vì $\widehat{BAC}$ là góc tù nên H nằm ngoài đoạn thẳng AC

Khi đó BA,BN,BC là đường xiên kẻ từ B đến AC,HA,HN,HC lần lượt là các hình chiếu của BA,BN,BC trên AC

Ta có: HA < HN < HC nên BA < BN < BC (quan hệ giữa đường xiên và hình chiếu)

Từ C kẻ CK vuông góc với AC, vì $\widehat{BAC}$ là góc tù nên K nằm ngoài đoạn thẳng AB

Khi đó CA,CM,CB à các đường xiên kẻ từ C đém AB,AK,KM,KB lần lượt là các hình chiếu của CA,CM,CB trên AB

Ta có: KA < KM < KB nên CA < CM < CB (quan hệ giữa đường xiên và hình chiếu)

Bài tập 3:

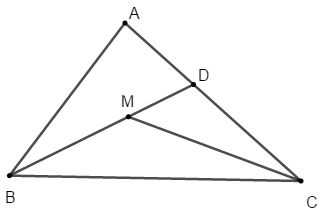
Vì M là điểm nằm trong tam giác ABC và BM cắt AC tại D nên M nằm giữa hai điểm B và D

Nên ta có: BD = BM + MD

Trong tam giác MDC ta có:

MC < MD + DC (bất đẳng thức trong tam giác)

MB + MC < MB + MD + DC

MB + MC < (BM + MD) + DC

MB + MC < BD + DC