Bài tập dạng Đường trung trực - Đường trung tuyến - Đường cao - Đường phân giác của tam giác

Bài tập 1: 

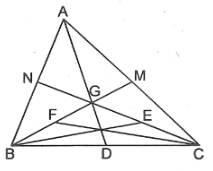
Gọi D là giao điểm của AG và BC. Vì G là trọng tâm của $\Delta ABC$ nên AD là đường trung tuyến, suy ra DB = DC

Ta có $GF = DM =\frac{1}{3}BM; GE = GN =\frac{1}{3}CN$

Do đó $GF = FB; GE = EC$

Xét $\Delta GBC$ có GD, BE, CF là ba đường trung tuyến nên chúng đồng quy suy ra ba đường thẳng AD, BE, CF đồng quy.

Bài tập 2:

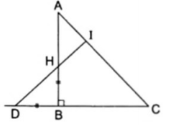
a) $\Delta ABC$ vuông cân tại B nên $\hat{C}=45^{o}$

$\Delta BDH$ có $\hat{B}=90^{o}$; BH = BD

Do đó $\Delta BDH$ vuông cân tại B, suy ra $\hat{D}=45^{o}$

$\Delta DIC$ có $\hat{D}+\hat{C}=45^{o}+45^{o}=90^{o}$

Do đó $DH \perp AC$

b) $\Delta ADC$ có $AB \perp BC; DH \perp AC$

Suy ra H là trực tâm của $\Delta ADC$, suy ra CH cũng là đường cao của tam giác.

Do đó $CH \perp AD$

Bài tập 3: 

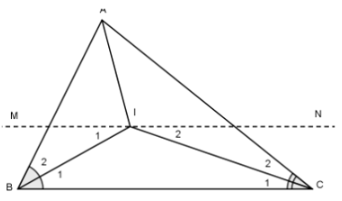
Ba phân giác của một tam giác cùng đi qua một điểm nên CI là tia phân giác của góc C

Vì MN // BC nên $\hat{C_{1}}=\hat{I_{1}}$

Mà $\hat{C_{1}} =\hat{C_{2}}$ nên $\hat{C_{2}} =\hat{I_{1}}$

Do đó $\Delta NIC$ cân nên NC = NI

Tương tự ta có MB = MI

Suy ra MI + IN = BM + CN

hay MN = BM + CN