TRẮC NGHIỆM

Câu 1: Tâm và bán kính đường tròn ngoại tiếp tam giác được xác định như thế nào?

• A. Tâm đường tròn ngoại tiếp tam giác là trung điểm của cạnh tam giác có hai đỉnh mà đường tròn đi qua. Bán kính đường tròn ngoại tiếp tam giác bằng một phần hai cạnh tam giác có hai đỉnh mà đường tròn đi qua.
• B. Tâm đường tròn ngoại tiếp tam giác là trọng tâm của tam giác đó. Bán kính đường tròn ngoại tiếp tam giác bằng khoảng cách từ giao điểm của trọng tâm đến đỉnh mà đường tròn đi qua của tam giác đó.
• C. Tâm đường tròn ngoại tiếp tam giác là trọng tâm của tam giác đó. Bán kính đường tròn ngoại tiếp tam giác bằng khoảng cách từ trọng tâm đến cạnh có hai đỉnh mà đường tròn đi qua.

• D. Tâm đường tròn ngoại tiếp tam giác là giao điểm ba đường trung trực của tam giác đó. Bán kính đường tròn ngoại tiếp tam giác bằng khoảng cách từ giao điểm ba đường trung trực đến mỗi đỉnh của tam giác đó.

Câu 2: Trong các hình dưới đây, hãy cho biết đâu là hình xác định đúng tâm đường tròn ngoại tiếp tam giác vuông?

Hình 1	Hình 2
Hình 3	Hình 4

• A. Hình 1, Hình 2, Hình 3
• B. Hình 1, Hình 2, Hình 4
• C. Hình 1, Hình 2

• D. Hình 1, Hình 3

Câu 3: Cho tam giác vuông ABC vuông tại A có AB = a cm; AC = b cm; BC = c cm. Tìm đường tròn ngoại tiếp tam giác ABC (ghi rõ vị trí tâm và độ dài bán kính đường tròn).

• A. Đường tròn ngoại tiếp tam giác ABC có tâm O là trọng tâm của tam giác ABC và bán kính R = OA = OB = OC = cm

• B. Đường tròn ngoại tiếp tam giác ABC có tâm O là trung điểm của BC và bán kính R = 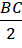= cm.

• C. Đường tròn ngoại tiếp tam giác ABC có tâm là điểm A và bán kính R = AB = a cm
• D. Đường tròn ngoại tiếp tam giác ABC có tâm là điểm A và bán kính R = AC = b cm

Câu 4: Cho bán kính đường tròn ngoại tiếp tam giác đều là 15 cm. Cạnh của tam giác đều đó bằng bao nhiêu? 

• A. 45 cm
• B. 15 cm

• C. 15 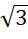cm

• D. 45 cm

Câu 5: Hãy cho biết đâu là hình ảnh vẽ đường tròn (O) ngoại tiếp tam giác MNP trong trường hợp . 

• A.
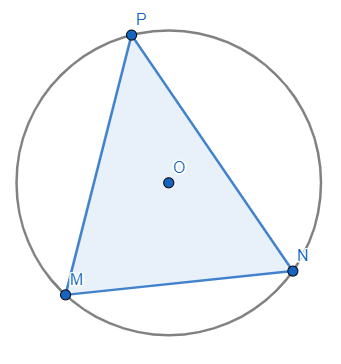
• B.
• C.

• D.

Câu 6:  Cho tam giác ABC vuông tại A, có AB = 9 cm, AC = 12 cm. Gọi I là tâm đường tròn nội tiếp, G là trọng tâm của tam giác. Tính độ dài IG

• A. 1 cm

• B. 1 m
• C. 2 cm
• D. 2 m

Câu 7: Cho tam giác ABC vuông tại A ngoại tiếp đường tròn (O). Gọi D, E, F lần lượt là các tiếp điểm của (O) với các cạnh AB, AC và BC. Đường thẳng BO cắt đường thẳng EF tại I. Tính góc BIF?

• A.
• B.

• C.

• D.

Câu 8: Thế nào được gọi là một tứ giác nội tiếp đường tròn?

• A.  Tứ giác có ít nhất một đỉnh thuộc một đường tròn được gọi là tứ giác nội tiếp đường tròn (hay còn gọi là tứ giác nội tiếp).
• B. Tứ giác có hai đỉnh thuộc một đường tròn được gọi là tứ giác nội tiếp đường tròn (hay còn gọi là tứ giác nội tiếp).
• C. Tứ giác có ba đỉnh thuộc một đường tròn được gọi là tứ giác nội tiếp đường tròn (hay còn gọi là tứ giác nội tiếp).

• D. Tứ giác có bốn đỉnh thuộc một đường tròn được gọi là tứ giác nội tiếp đường tròn (hay còn gọi là tứ giác nội tiếp).

Câu 9: Bán kính của đường tròn ngoại tiếp hình vuông cạnh a là gì?

• A. Bán kính của đường tròn ngoại tiếp hình vuông cạnh a bằng chính a.
• B. Bán kính của đường tròn ngoại tiếp hình vuông cạnh a bằng .

• C. Bán kính của đường tròn ngoại tiếp hình vuông cạnh a bằng .

• D. Bán kính của đường tròn ngoại tiếp hình vuông cạnh a bằng .

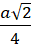Câu 10: Chọn phát biểu sai?

• A. Tứ giác có hai góc đối diện đều bằng 90 thì tâm đường tròn ngoại tiếp tứ giác đó là trung điểm của cạnh đối diện hai góc vuông đó.
• B. Tứ giác có hai đỉnh kề nhau và cùng có số đo bằng 90 đồng thời cùng nhìn dưới một cạnh thì tứ giác đó nội tiếp được tròn.

• C. Hình thang cân không phải là một tứ giác nội tiếp đường tròn.

• D. Trong một đường tròn, hai dây không đi qua tâm không thể cắt nhau tại trung điểm của mỗi đường.

Câu 11: Tìm trong hình vẽ sau:

• A. 105.8

• B. 74.2

• C. 52.9
• D. 37.1

Câu 12: Cho tứ giác ABCD nội tiếp đường tròn. Tính số đo mỗi góc của tứ giác biết rằng và .

• A.

• B.
• C.
• D.

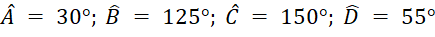
Câu 13: Tứ giác ABCD có AB//CD, và nội tiếp đường tròn. Hãy cho biết tứ giác là hình gì và số đo 3 góc còn lại bằng bao nhiêu?

• A. Tứ giác là hình thoi và

• B. Tứ giác là hình thang cân và

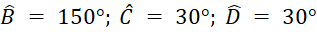
• C. Tứ giác là hình thang và
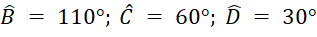
• D. Tứ giác là hình bình hành và

Câu 14: Quan sát hình dưới đây và cho biết số đo góc DBC là bao nhiêu biết số đo góc DEA là 108?

• A. 130
• B. 72

• C. 58

• D. 42

Câu 15: Cho hình vuông ABCD, ta lấy lần lượt các điểm M, N trên các cạnh BC và CD sao cho góc MAN có số đô là 45. Đường thẳng BD cắt các đường thẳng AM, An tương ứng tại các điểm P, Q. Hãy cho biết vị trí tương đối các các điểm M, N, Q, P, C.

• A. M, N, Q, P, C cùng nằm trên một đường tròn.

• B. M, N, Q, P cùng nằm trên một đường tròn, C nằm bên ngoài đường tròn đó.
• C. M, N, Q, P cùng nằm trên một đường tròn, C nằm bên trong đường tròn đó.
• D. M, N, Q cùng nằm trên một đường tròn, C và P không nằm trên đường tròn đó.

Trên nửa đường tròn tâm O đường kính AB = 2R, lấy điểm C (C khác A và B), từ C kẻ CH vuông góc với AB (. Gọi D là điểm bất kì trên đoạn CH (D khác C và H), đường thẳng AD cắt nửa đường tròn tại điểm thứ hai là E. Sử dụng dữ kiện này để trả lời hai câu hỏi: (câu 1-câu 2)

Câu 16: Biểu thức nào dưới đây là đúng?

• A. = CD.AC

• B. AD.EC = CD.AC

• C. = AD.EC
• D. AD.CD = EC.AC

Câu 17: Khi điểm C di chuyển trên nửa đường tròn (C khác A, B và là điểm nằm giữa cung AB), xác định vị trí của điểm C sao cho chu vi tam giác COH đạt giá trị lớn nhất và giá trị đó bằng bao nhiêu.

• A. Chu vi tam giác COH đạt giá trị lớn nhất bằng khi điểm C nằm trên nửa đường tròn đường kính AB sao cho .
• B. Chu vi tam giác COH đạt giá trị lớn nhất bằng khi điểm C nằm trên nửa đường tròn đường kính AB sao cho . 
• C. Chu vi tam giác COH đạt giá trị lớn nhất bằng khi điểm C nằm trên nửa đường tròn đường kính AB sao cho .

• D. Chu vi tam giác COH đạt giá trị lớn nhất bằng  khi điểm C nằm trên nửa đường tròn đường kính AB sao cho .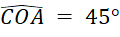

Đề bài: Giáo viên yêu cầu xác định đường tròn ngoại tiếp tam giác (tâm và bán kính) ABC có AB > AC. Dưới dây là bài làm của 4 bạn Ly, Bắc, Quỳnh Anh, Trường. 

Ly làm như sau:  - Bước 1: Kẻ ba đường trung trực của ba cạnh AB, AC, BC. Giao điểm của ba đường trung trực là tâm O của đường tròn ngoại tiếp tam giác ABC. - Bước 2: Nối O với A ta được bán kính R = OA. - Bước 3: Hoàn thiện đường tròn với tâm O, bán kính OA ta được đường tròn ngoại tiếp tam giác ABC
Bắc làm như sau:  - Bước 1: Kẻ các đường cao hạ từ ba đỉnh A, B, C của tam giac. Giao điểm ba đường cao chính là tâm O của đường tròn ngoại tiếp. - Bước 2: Kiểm tra OA, OB, OC, đoạn nào có độ dài lớn nhất là bán kính của đường tròn ngoại tiếp (R = OC). - Bước 3: Hoàn thiện đường tròn với tâm là O, bán kính là OC ta được đường tròn ngoại tiếp tam giác ABC.
Quỳnh Anh làm như sau:  - Bước 1: Kẻ các đường trung tuyến hạ từ ba đỉnh A, B, C của tam giác. Giao điểm ba đường trung tuyến chính là tâm O của đường tròn ngoại tiếp. - Bước 2: Kiểm tra xem OA, OB, OC, đoạn nào có độ dài lớn nhất là bán kính của đường tròn ngoại tiếp (R = OC). - Bước 3: Hoàn thiện đường tròn với tâm là O, bán kính là OC ta được đường tròn ngoại tiếp tam giác.
Bạn Trường làm như sau:  - Bước 1: Kẻ hai đường trung trực của hai cạnh AB và BC. Giao điểm của hai đường đó là tâm O của đường tròn ngoại tiếp tam giác ABC. - Bước 2: Nối O với B ta được bán kính R = OB. - Bước 3: Hoàn thiện đường tròn với tâm O, bán kính OB ta được đường tròn ngoại tiếp tam giác ABC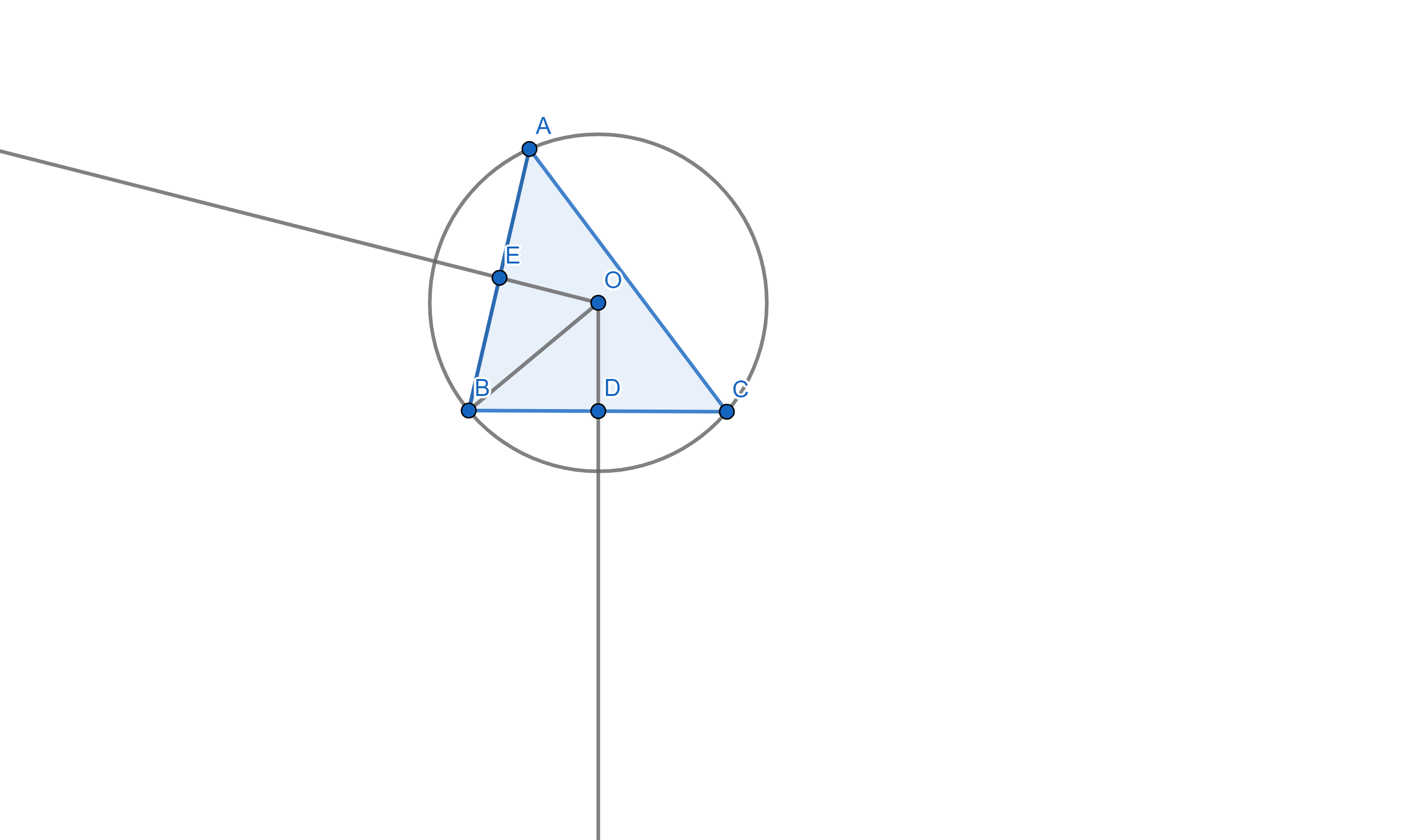

Hãy sử dụng dữ diện trên để trả lời các câu hỏi 18, 19, 20.

Câu 18: Trong các bài làm trên, có bao nhiêu bài làm đúng?

• A. 1

• B. 2

• C. 3 
• D. 4

Câu 19: Hãy cho biết trong số các bạn làm sai có bạn Bắc hay không, nếu có hãy sửa bài của bạn ấy.

• A. Bạn Bắc làm đúng.
• B. Bạn Bắc làm sai, sửa từ bước 2 thành kiểm tra xem đoạn nào có độ dài nhỏ nhất là bán kính của đường tròn ngoại tiếp tam giác ABC (R = OA)
• C. Bạn Bắc làm sai, sửa từ bước 1 thành “Kẻ các đường trung tuyến hạ từ ba đỉnh A, B, C của tam giác. Giao điểm ba đường trung tuyến chính là tâm O của đường tròn ngoại tiếp tam giác ABC.”, sửa bước 2 thành “Kiểm tra xem OA, OB, OC, đoạn nào có độ dài nhỏ nhất là bán kính của đường tròn ngoại tiếp (R = OA)”

• D. Bạn Bắc làm sai, sửa từ bước 1 thành “Kẻ các đường trung trực của các cạnh AB, AC, BC. Giao điểm ba đường trung trực là tâm O của đường tròn ngoại tiếp tam giác ABC.”, sửa bước 2 thành “Nối O với C, ta được bán kính của đường tròn ngoại tiếp tam giác ABC (R = OC).”

Câu 20: Nêu từng lỗi sai mà các bạn làm sai đang mắc phải?

• A. Bạn Bắc và bạn Quỳnh Anh xác định sai tâm và bán kính đường tròn ngoại tiếp tam giác ABC.

• B. Bạn Ly và Trường xác định sai tâm đường tròn ngoại tiếp tam giác ABC.
• C. Bạn Ly và Bắc xác định sai tâm đường tròn ngoại tiếp tam giác ABC.
• D. Bạn Trường và Quỳnh Anh xác định sai bán kính của đường tròn ngoại tiếp tam giác ABC.

Câu 21: Cho hình thoi ABCD. Giao điểm của AC và BD là I. Đường tròn đi qua ba điểm A, I, D cắt CD tại M. Hãy chọn phát biểu đúng.

• A.

• B.

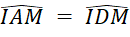
• C. Tam giác AMD nội tiếp đường tròn tâm là trung điểm của ID.
• D.

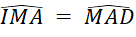
Câu 22: Cho tam giác đều có . Bán kính đường tròn nội tiếp bằng bao nhiêu?

• A. cm

• B. cm

• C. . cm
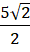• D. . cm

Câu 23: Cho tam giác vuông tại có , bán kính đường tròn nội tiếp tam giác là r, bán kính đường tròn ngoại tiếp tam giác là R. Tính

• A.

• B.
• C.
• D.

Câu 24: Cho hình chữ nhật có . Bán kính đường tròn ngoại tiếp tam giác là R, bán kính đường tròn nội tiếp tam giác là r và bán kính đường tròn ngoại tiếp hình chữ nhật là R’. Tính A =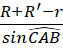

• A.

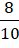
• B. 10.

• C. 8.
• D. .

Câu 25: Cho tam giác nhọn nội tiếp đường tròn (O). Hai đường cao cắt nhau tại (). Quan hệ giữa hai cạnh và là gì?

• A.
• B.

• C.

• D. và cắt nhau và không vuông góc. 

Câu 26: Cho nửa đường tròn (O) đường kính AB. Vẽ tiếp tuyến AM cùng phía với nửa đường tròn (O). Từ M, vẽ tiếp tuyến MC với nửa đường tròn (O) (C là tiếp điểm). Vẽ AC cắt OM tại E, vẽ MB cắt nửa đường tròn (O) tại D (D B). Vẽ CH vuông góc với AB (H AB). Hãy cho biết MB cắt đoạn thẳng CH tại điểm có đặc điểm như thế nào?

• A. MB cắt CH tại I là tâm đường tròn ngoại tiếp tam giác OCH.
• B. MB cắt CH tại I là tâm đường tròn ngoại tiếp tứ giác DCHE.
• C. MB cắt CH tại I với IC = CH

• D. MB cắt CH tại I là trung điểm của CH.