ĐỀ 2
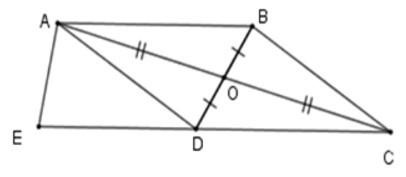
Câu 1: Cho hình bình hành ABCD có $\widehat{A} = \alpha > 90^{\circ}$. Ở phía ngoài hình bình hành vẽ các tam giác đều ADE, ABF. Tam giác CEF là tam giác gì? Chọn câu trả lời đúng nhất
- A. Tam giác
- B. Tam giác tù
- C. Tam giác cân
- D. Tam giác đều
Câu 2: Hãy chọn câu đúng. Tứ giác ABCD là hình bình hành nếu.
- A. $\widehat{A}=\widehat{C}$
- B. BC = AD
- C. AB = CD, BC = AD
- D. AB // CD
Câu 3: Hãy chọn câu sai.
- A. Hình bình hành có hai góc đối bằng nhau
- B. Hình bình hành có hai đường chéo cắt nhau tại trung điểm mỗi đường
- C. Hình bình hành có hai đường chéo vuông góc với nhau
- D. Hai bình hành có hai cặp cạnh đối song song
Câu 4: Chọn phương án đúng trong các phương án sau.
- A. Hình bình hành là tứ giác có các cạnh đối song song.
- B. Hình bình hành là tứ giác có các góc bằng nhau.
- C. Hình bình hành là tứ giác có hai cạnh đối song song.
- D. Hình bình hành là hình thang có hai cạnh kề bằng nhau.
Câu 5: Cho hình thang ABCD có AD // BC và $\widehat{BAD} = 100^{\circ}; \widehat{ADC} = 80^{\circ}$. Tìm khẳng định sai
A. AB// CD
B. Tứ giác ABCD là hình bình hành
C. AC = BD
D. AB = CD; AD = BC
Câu 6: Cho hình bình hành ABCD. Tia phân giác của góc A cắt CD tại M. Tia phân giác góc C cắt AB tại N (hình vẽ). Hãy chọn câu trả lời sai.

- A. ANCD là hình thang cân
- B. CMBA là hình thang
- C. AMCN là hình bình hành
- D. AN = MC
Câu 7: Hãy chọn câu đúng. Cho hình bình hành ABCD có các điều kiện như hình vẽ, trong hình có:
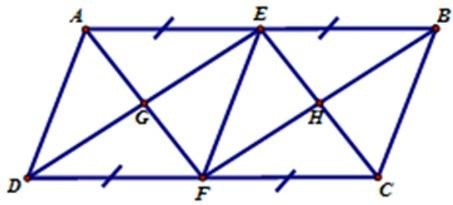
- A. 5 hình bình hành
- B. 6 hình bình hành
- C. 4 hình bình hành
- D. 3 hình bình hành
Câu 8: Cho tứ giác ABCD. Gọi E, F lần lượt là giao điểm của AB và CD; M, N, P, Q lần lượt là trung điểm của AF, EC, BF, DE. Khi đó MNPQ là hình gì? Chọn đáp án đúng nhất.
- A. Hình thang
- B. Hình thang cân
- C. Hình thang vuông
- D. Hình bình hành
Câu 9: Chọn câu sai. ABCD là hình bình hành. Khi đó:
- A. AB = CD
- B. AD = BC
- C. AC = BD
- D. $\widehat{A}=\widehat{C};\widehat{B}=\widehat{D}$
Câu 10: Cho tam giác ABC có BC = 6cm. Trên cạnh AB lấy các điểm D và E sao cho AD = BE. Qua D, E lần lượt vẽ các đường thẳng song song với BC, cắt AC theo thứ tự ở G và H. Tính tổng DG + EH.
- A. 10cm
- B. 6cm
- C. 8cm
- D. 4cm




Bình luận