Đề số 4: Đề kiểm tra toán 8 Kết nối bài 12 Hình bình hành

Câu 1

Xét 2 tam giác OAD và OCB có:

$\widehat{OAD}=\widehat{0CB}$ (gt)

OA = OC (gt)

$\widehat{AOD}=\widehat{COB}$ (2 góc đối đỉnh)

=> Tam giác OAD= tam giác OCB bằng nhau (g-c-g)

=> OC = OD.

Vậy tứ giác ABCD có 2 đường chéo cắt nhau tại trung điểm mỗi đường nên sẽ là hình bình hành.

Câu 2

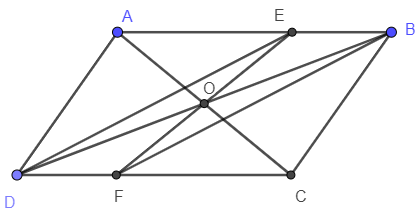
Ta có

$ED=\frac{1}{2}AD$ (E là trung điểm của AD)

$BF=\frac{1}{2}BC$ (F là trung điểm của BC)

Mà AD = BC (ABCD là hình bình hành)

=> ED = BF

Mà ED // BF (AD // BC, $E\in AD;F\in BC$)

Do đó tứ giác EBFD là hình bình hành.