ĐỀ 2

Câu 1: Tìm tất cả các giá trị của tham số m để hàm số $y=\frac{m+3}{m-3}x-\sqrt{5}$ là hàm số bậc nhất

• A. $m\neq 3$
• B. $m\neq 3$ và $m\neq -3$
• C. $m\neq -3$
• D. $m=-3$

Câu 2: Trong các hàm số $y=3x-2; y=\sqrt{3}(x+1)-5; y=\frac{1}{2x}+6; y=-1,5x$, hàm số không phải hàm số bậc nhất là

• A. $y=\sqrt{3}(x+1)-5$
• B. $y=3x-2$
• C. $y=\frac{1}{2x}+6$
• D. $y=-1,5x$

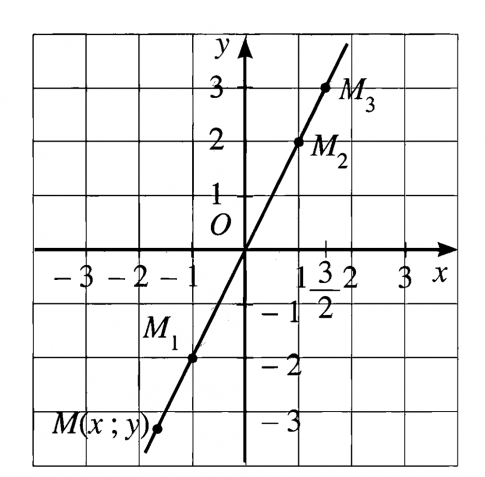
Câu 3: Đồ thị hàm số $y=2x$ đi qua điểm nào?

• A. (1;2)
• B. (2;2)
• C. (-2;-1)
• D. (2;1)

Câu 4: Điểm $A(\sqrt{2};3)$ thuộc đồ thị hàm số nảo?

• A. $y=\sqrt{2}x+1$
• B. $y=\sqrt{2}x-1$
• C. $y=-\sqrt{2}x+1$
• D. $y=-5x+4$

Câu 5: Đồ thị của hàm số $y=2x+3$ là đường thẳng đi qua hai điểm phản biệt sau

• A. $(0;3) và \left ( -\frac{3}{2};0 \right )$
• B. $(0;3) và (3;0)$
• C. $(0;3) và \left ( -\frac{3}{2};2 \right )$
• D. $(3;0) và \left ( -\frac{3}{2};0 \right )$

Câu 6: Tìm a và b để đồ thị hàm số $y=ax+b$ đi qua các điểm A(-2;1), B(1;-2)

• A. a = -2 và b = -1
• B. a = 2 và b = 1
• C. a = 1 và b = 1
• D. a = -1 và b = -1

Câu 7: Trong mặt phẳng tọa độ Oxy, tập nghiệm của phương trình 4x+y=1 được biểu diển bởi đồ thị hàm số nào đưới đây?

• A. $y=-4x+1$
• B. $y=4x+1$
• C. $y=4x-1$
• D. $y=-4x-1$

Câu 8: Cho hàm số bậc nhất $y=\sqrt{3}x$ có đồ thị d , khẳng định nào sau đây sai?

• A. Điểm $E\left ( \frac{1}{\sqrt{6}};\frac{1}{\sqrt{2}} \right )$ thuộc d.
• B. Điểm H thuộc d có tung độ là $\sqrt{12}$ thì hoành độ của  là 2.
• C. Đường thẳng d cắt trục hoành tại điểm có hoành độ $\sqrt{3}$
• D. Điểm I thuộc d có hoành độ $-\sqrt{3}$ thì tung độ của I là -3

Câu 9: Một xe khách khởi hành từ bến xe phía Nam bưu điện thành phố Hà Nội để đi về thành phố Thái Bình với tốc độ 40km/h theo hình bên.

Biết rằng xe khách cách bưu điện thành phố Hà Nội 5km. Sau x giờ xe khách cách bưu điện thành phố Hà Nội y km. Tính y theo x.

• A. y = 40x+5
• B. y = 40x
• C. y = 5x+40
• D. y = 5x

Câu 10: Hàm số $y=\left | -x-3 \right |+\left | 2x+1 \right |+\left |  x+1\right |$ đồng biến trong khoảng nào?

• A. $(-∞; -\frac{1}{2}).$
• B. $(-∞; \frac{1}{2}).$
• C. $(\frac{1}{2}; +∞).$
• D. $(-\frac{1}{2}; +∞).$

ĐỀ 4

Câu 1 (6 điểm).

a) Vẽ đồ thị hàm số $y=3x+2.$

b) Gọi A, B lần lượt là giao điểm của đồ thị hàm số trên trục tung và trục hoành.

Tính diện tích tam giác OAB.

Câu 2 (4 điểm). Trong mặt phẳng tọa độ Oxy cho ba đường thẳng:

$(d_{1}): 2x-y+3=0$

$(d_{2}): 15x+3y+5=0$

$(d_{3}):3ax-3y+4a+9=0$

a) Tìm a để ba đường thẳng có một điểm chung.

b) Với giá trị của a vừa tìm được, hãy tính chu vi và diện tích của tam giác tạo bởi $(d_{3})$ với các trục Ox, Oy.