Đề số 6: Đề kiểm tra toán 8 Kết nối bài 28 Hàm số bậc nhất và đồ thị của hàm số bậc nhất
ĐỀ 6
I. Phần trắc nghiệm (4 điểm)
Câu 1: Đồ thị hàm số $y=2x-1$ cắt trục tung tại điểm nào?
- A. (0;-1)
- B. (1;1)
- C. (0;2)
- D. $(0;\frac{1}{2})$
Câu 2: Đồ thị hàm số $y=3x+6$ cắt trục hoảnh tại điểm nào?
- A. (2;0)
- B. (-3;0)
- C. (-2;0)
- D. (0;6)
Câu 3: Đồ thị nào dưới đây là đồ thị hàm số y = 2x – 1.
- A.
- B.
- C.
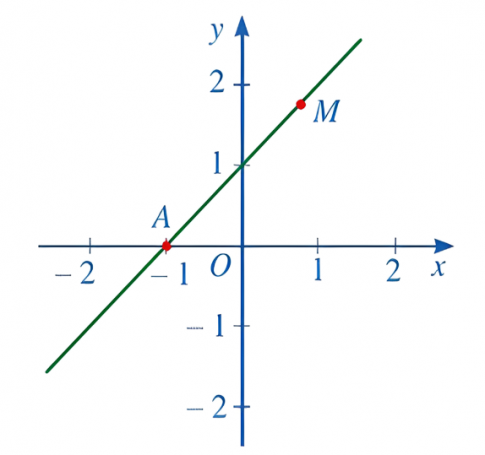
- D.
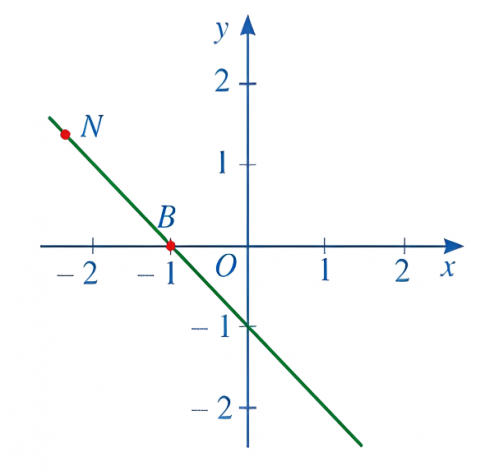
Câu 4: Tìm toạ độ điểm D trong mặt phẳng toạ độ Oxy sao cho A (4; 1); B (2; 3); C (6 ; 2) và D lập thành hình bình hành ABCD.
- A. D (6; 3).
- B. D (1; 4).
- C. D (4; 5).
- D. D (8; 0).
II. Phần tự luận (6 điểm)
Câu 1 (4 điểm): Trong hệ trục toạ độ Oxy cho hàm số $y=2x+m$ (*)
Tìm giá trị của m để đồ thị hàm số đi qua:
a) A(-1;3)
b) $B(\sqrt{2};-5\sqrt{2})$
Câu 2 (2 điểm): Cho hàm số f(x)=ax+b. Xác định a+b, biết f(x-1)=-x+3, với mọi $x \in \mathbb{R}$
Câu 1:
Đồ thị hàm số $y=2x+m$ đi qua A(-1;3)
$<=> 3=2(-2)+m$
$<=> 3=-2+m$
$<=> m=5$
Vậy với $m=5$ thì đồ thị hàm số $y=2x+m$ đi qua $A(-1;3)$
b) Để đồ thị hàm số $y=2x+m$ đi qua $B(\sqrt{2};-5\sqrt{2})$
$<=> -5\sqrt{2}=2\sqrt{2}+m$
$<=> m=-7\sqrt{2}$
Vậy với $m=-7\sqrt{2}$ thì đồ thị hàm $y=2x+m$ đi qua $B(\sqrt{2};-5\sqrt{2})$
Câu 2
Ta có: $f(x−1)=-x+3$
$<=> a(x-1)+b=-x+3$
$<=> ax-a+b=-x+3$
$<=> a = -1 và -a+b=3$
$<=> a=-1 và b=2$
Vậy $a+b=1.$
Giải những bài tập khác
Giải bài tập những môn khác
Giải sgk lớp 8 cánh diều
Giải SBT lớp 8 kết nối tri thức
Giải SBT lớp 8 chân trời sáng tạo
Soạn SBT lớp 8 cánh diều
Trắc nghiệm 8 Kết nối tri thức
Trắc nghiệm 8 Chân trời sáng tạo
Trắc nghiệm 8 Cánh diều
Bộ đề thi, đề kiểm tra lớp 8 chân trời sáng tạo
Giáo án lớp 8
Bình luận