Đề số 4: Đề kiểm tra toán 8 Kết nối bài 28 Hàm số bậc nhất và đồ thị của hàm số bậc nhất

Câu 1

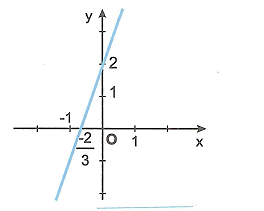
a) Vẽ đồ thị hàm số $y=3x+2$

Đồ thị đi qua $A(0;2)$ và $B(-\frac{2}{3};0)$

b) Ta có $S_{OAB}=\frac{1}{2}OA.OB=\frac{1}{2}\left | 2.\frac{-2}{3} \right |=\frac{2}{3}$ (đvdt)

Vậy diện tích tam giác OAB là $\frac{2}{3}$ (đvdt)

Câu 2

a) Tọa độ giao điểm của $(d_{1})$ và $(d_{2})$ là nghiệm của hệ phương trình:

$\left\{\begin{matrix}2x-y+3=0\\ 15x+3y+5=0\end{matrix}\right.$

$<=> \left\{\begin{matrix}x=\frac{-2}{3}\\ y=\frac{5}{3}\end{matrix}\right.$

Thay $x=\frac{-2}{3}; y=\frac{5}{3}$ vào phương trình $(d_{3}): 3ax-3y+4a+9=0$ ta được $a=-2$

b) Với $a=-2$ thì $(d_{3}): -6x-3y+1=0$

Từ đó ta tính được đường thẳng $(d_{3})$ cắt trục hoành tại $A\left ( \frac{1}{6};0 \right )$ , cắt trục tung tại $B\left ( 0;\frac{1}{3} \right )$

$=> AB=\frac{1}{6}\sqrt{5}$

Chu vi tam giác OAB là: $\frac{1}{2}+\frac{1}{6}\sqrt{5}$

Diện tích tam giác OAB là: $\frac{1}{36}$