BÀI 28. HÀM SỐ BẬC NHẤT VÀ ĐỒ THỊ CỦA HÀM SỐ BẬC NHẤT (2 tiết)

I. KHÁI NIỆM HÀM SỐ BẬC NHẤT

HĐ1

- Sau t giờ ô tô đi được: S=60.t (km)

- Ta thấy quãng đường S là một hàm số của thời gian t.

HĐ2

- Từ Trung tâm Hà Nội đến bến xe Giáp Bát là: 7 km

- Quãng đường ô tô di chuyển được sau t giờ là: 60.t (km)

- Khoảng cách d từ vị trí của ô tô đến trung tâm Hà Nội sau t giờ là: d=60t+7

HĐ3

Ta thấy khoảng cách d là một hàm số của thời gian t.

Khái niệm

Hàm số bậc nhất là hàm số cho bởi công thức y=ax+b, trong đó a, b là các số cho trước và a≠0.

Ví dụ 1: (SGK – tr.47)

Hướng dẫn giải (SGK – tr.47)

Câu hỏi

- Các hàm số là hàm số bậc nhất: a); b); d)

Ví dụ 2: (SGK – tr.48)

Hướng dẫn giải (SGK – tr.48)

Vận dụng

a) Công thức chuyển đổi x (dặm) sang y (km):

y=1,609 . x

Công thức tính y theo x chính là một hàm số bậc nhất của x.

b) Đổi 55 (dặm) =55.1,609=88,495 (km)

Thấy rằng 88,495>80.

Vậy ô tô đó đã vi phạm luật giao thông.

Tranh luận

Xét hàm số y=$\frac{x+1}{2}$=$\frac{x}{2}$+$\frac{1}{2}$=$\frac{1}{2}$.x+$\frac{1}{2}$

Vậy đây là một hàm số bậc nhất với a=b=$\frac{1}{2}$

Vậy Vuông đúng.

II. ĐỒ THỊ CỦA HÀM SỐ BẬC NHẤT

Nhận biết đồ thị của hàm số bậc nhất

HĐ4

HĐ5

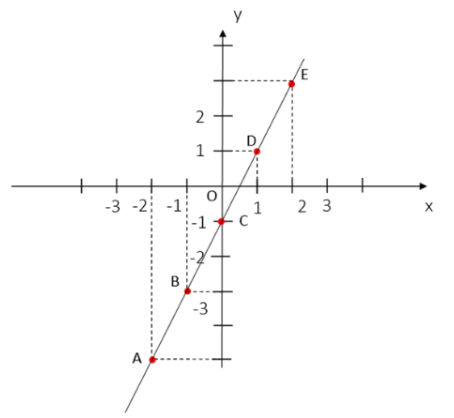
Tung độ các điểm A, B, C, D, E chính là giá trị của y tương ứng với x trong bảng HĐ4.

Vậy tọa độ các điểm là: A(-2;-5);B(-1;-3);C(0; -1);D(1;1);E(2;3)

HĐ6

Khái niệm

Đồ thị của hàm số y=ax+b (a≠0) là một đường thẳng

Đồ thị của hàm số y=ax+b a≠0 còn được gọi là đường thẳng y=ax+b (a≠0)

Cách vẽ đồ thị của hàm số bậc nhất

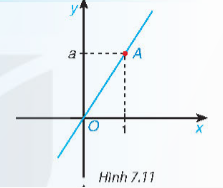
* Trường hợp 1: Khi b=0 thì hàm số trở thành y=ax là đường đi qua góc O(0;0) và A(1;a)

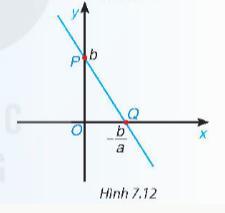
* Trường hợp 2: Khi b≠0 ta phải xác định các điểm mà đồ thị đi qua:

+ Cho x=0 thì y=b, được điểm P0;b thuộc trục tung Oy

+ Cho y=0 thì x=-ba, được điểm Q-ba;0 thuộc trục hoành Ox.

+ Vẽ đường thẳng d đi qua hai diểm P, Q ta được đồ thị hàm số y=ax+b (a≠0) 

Ví dụ 3: (SGK – tr.49)

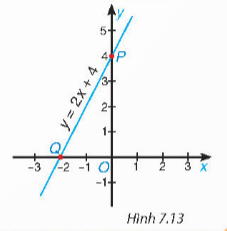
Hướng dẫn giải (SGK – tr.49)

Luyện tập

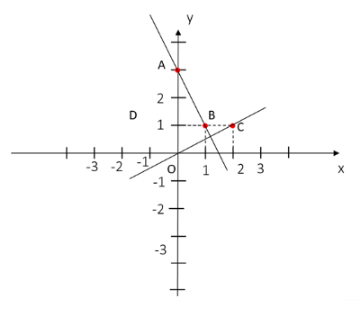
* Hàm số: y=-2x+3

+ Hàm số đi qua điểm A(0;3) và B1;1

* Hàm số: y=$\frac{1}{2}$x

+ Hàm số đi qua điểm O(0;0) và C(2;1)