Đề số 5: Đề kiểm tra toán 8 Kết nối bài 12 Hình bình hành
III. DẠNG 3 – ĐỀ TRẮC NGHIỆM VÀ TỰ LUẬN
ĐỀ 5
I. Phần trắc nghiệm (4 điểm)
(Chọn chữ cái trước câu trả lời đúng nhất.)
Câu 1: Cho hình bình hành ABCD có $\widehat{A}=3\widehat{B}$ Số đo các góc của hình bình hành là:
- A. $\widehat{A}=\widehat{C}=145^{\circ}; \widehat{B}=\widehat{D}=35^{\circ}$
- B. $\widehat{A}=\widehat{C}=125^{\circ}; \widehat{B}=\widehat{D}=55^{\circ}$
- C. $\widehat{A}=\widehat{C}=130^{\circ}; \widehat{B}=\widehat{D}=50^{\circ}$
- D. $\widehat{A}=\widehat{C}=135^{\circ}; \widehat{B}=\widehat{D}=45^{\circ}$
Câu 2: Chọn phương án sai trong các phương án sau?
- A. Tứ giác có các cạnh đối song song là hình bình hành.
- B. Tứ giác có các cạnh đối bằng nhau là hình bình hành.
- C. Tứ giác có hai góc đối bằng nhau là hình bình hành.
- D. Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
Câu 3: Tính số đo các góc của hình bình hành ABCD biết $\widehat{D}-\widehat{C} = 40^{\circ}.$ Ta đươc:
- A. $\widehat{A}=\widehat{C}=100^{\circ}; \widehat{B}=\widehat{D}=80^{\circ}$
- B. $\widehat{A}=\widehat{C}=80^{\circ}; \widehat{B}=\widehat{D}=100^{\circ}$
- C. $\widehat{A}=\widehat{C}=120^{\circ}; \widehat{B}=\widehat{D}=60^{\circ}$
- D. $\widehat{A}=\widehat{C}=70^{\circ}; \widehat{B}=\widehat{D}=110^{\circ}$
Câu 4: Cho hình bình hành ABCD. Gọi E, F theo thứ tự là trung điểm của AD, BC. Đường chéo AC cắt BE, DF theo thứ tự ở K, I. Chọn khẳng định đúng nhất.
- A. K, I lần lượt là trọng tâm ΔABD, ΔCBD
- B. AK = KI = BC
- C. Cả A, B đều đúng
- D. Cả A, B đều sai
II. Phần tự luận (6 điểm)
Câu 1 (6 điểm): Cho hình bình hành ABCD. Gọi I, K lần lượt là trung điểm của các cạnh AB và CD, E và F là giao điểm của AK và CI với BD. Chứng minh tứ giác AKCI là hình bình hành.
Trắc nghiệm: (Mỗi câu đúng tương ứng với 1 điểm)
Câu hỏi | Câu 1 | Câu 2 | Câu 3 | Câu 4 |
Đáp án | D | C | D | A |
Tự luận:
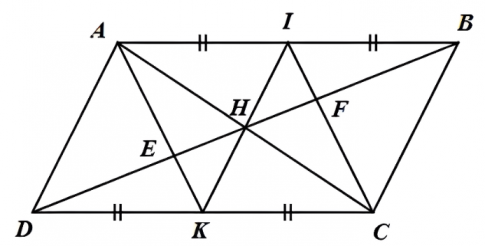
Ta có
$AI=\frac{1}{2}AB$ (I là trung điểm của AB),
$CK=\frac{1}{2}CD$ (K là trung điểm của CD)
Và AB = CD (ABCD là hình bình hành)
=> AI = CK
Mà AI // CK (AB // CD, I ∈ AB, K ∈ CD)
Do đó tứ giác AICK là hình bình hành.
Xem toàn bộ: Đề kiểm tra Toán 8 KNTT bài 12: Hình bình hành

Bình luận