BÀI 12. HÌNH BÌNH HÀNH

I. HÌNH BÌNH HÀNH VÀ TÍNH CHẤT

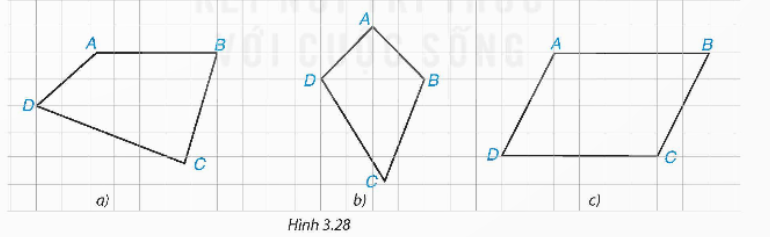
HĐ1. Trong hình 3.28, có một hình bình hành, đó là hình nào? Em có thể giải thích tại sao không?

Đáp án chuẩn:

Hình 3.28 c) là hình bình hành, vì có hai hai cặp cạnh đối song song với nhau

HĐ2. Hãy nêu các tính chất của hình bình hành mà em đã biết

Đáp án chuẩn:

- Các góc đối bằng nhau.

- Các cạnh đối song song và bằng nhau.

- Hai đường chéo cắt nhau tại trung điểm của mỗi đường.

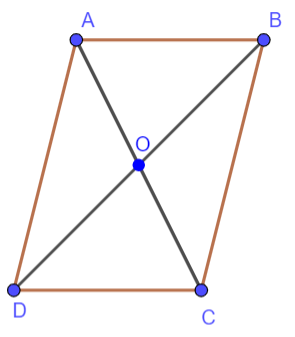
HĐ3. Cho hình bình hành ABCD (H3.30) Chứng minh = Từ đó suy ra AB = CD; AD = BC; Chứng minh =   Từ đó suy ra Gọi giao điểm của 2 đường chéo AC, BD là O. Chứng minh = OA = OC; OB = OD.

Đáp án chuẩn:

Ta có ABCD là hình bình hành.

a) = (g.c.g)

=> AB = CD; AD = BC; .

b) = (c.g.c).

=> .

c) = (g.c.g) => OA = OC; OB = OD.

LT 1. Cho tam giác ABC. Từ một điểm M tùy ý trên cạnh BC, kẻ đường thẳng song song với AB, cắt cạnh AC tại N và kẻ đường thẳng song song với AC, cắt AB tại P. Gọi I là trung điểm của đoạn NP. Chứng minh rằng I cũng là trung điểm của đoạn thẳng AM.

Đáp án chuẩn:

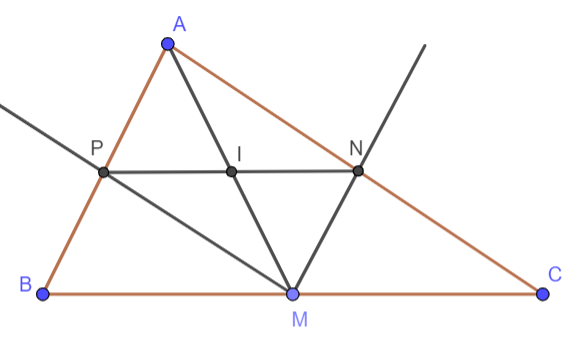
Chứng minh ANMP là hình bình hành

Mà I là trung điểm của PN  => I cũng là trung điểm của AM.

II. DẤU HIỆU NHẬN BIẾT

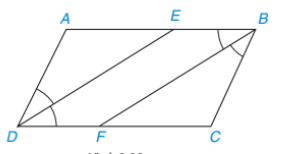
LT 2. Cho hình bình hành ABCD (AB >BC). Tia phân giác của góc D cắt AB tại E và tia phân giác của góc B cắt CD tại F (H.3.32)

1. Chứng minh hai tam giác ADE và CBF là những tam giác cân bằng nhau
2. Tứ giác DEBF là hình gì? Vì sao?

Đáp án chuẩn:

a) Chứng minh

=> cân tại A.

+) Chứng minh  

=> cân tại C.

+) Xét và có: AD = BC;  

=> = (g.c.g).

=> ED = BF (đpcm)

b) Tứ giác DEBF là hình bình hành vì ED = BF và ED // BF

LT 3. Cho hai điểm A, B phân biệt và điểm O không nằm trên đường thẳng AB. Gọi  A’, B’ là các điểm sao cho 0 là trung điểm của A,A’, BB’. Chứng minh rằng A’B’ = AB; A’B’ // AB.

Đáp án chuẩn:

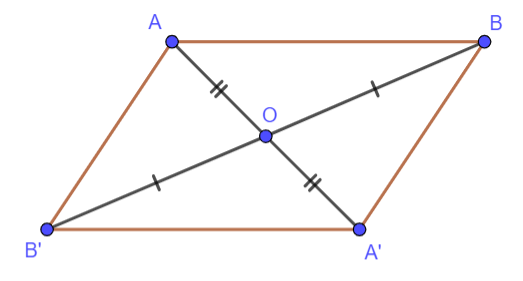
Tứ giác ABA'B' là hình bình hành 

=>A'B' = AB và A'B' // AB 

Vận dụng. Trở lại bài mở đầu. Em hãy vẽ hình và nêu các vẽ con đường cần mở.

Đáp án chuẩn:

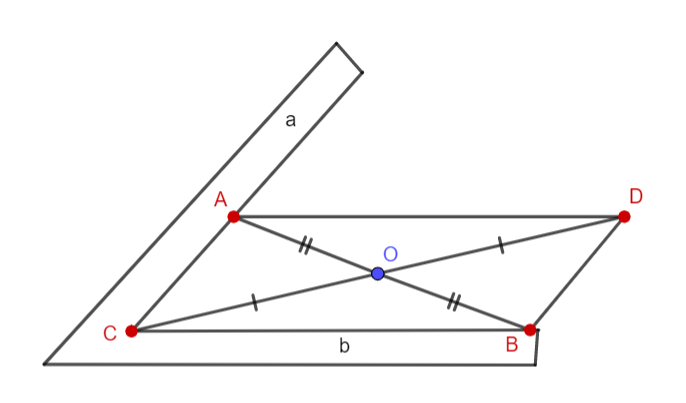
III. GIẢI BÀI TẬP CUỐI SGK

Bài 3.13. Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai? Vì sao?

1. Hình thang có hai cạnh bên song song là hình bình hành
2. Hình thang có hai cạnh bên bằng nhau là hình bình hành
3. Tứ giác có hai cạnh đối nào cũng song song là hình bình hành

Đáp án chuẩn:

a) Đúng, vì khi đó ta được tứ giác có các cạnh đối song song là hình bình hành 

b) Sai, vì hình thang cân có hai cạnh bên bằng nhau nhưng nó không phải là hình bình hành.

c) Đúng, vì khi đó ta được tứ giác có các cạnh đối song song là hình bình hành 

Bài 3.14. Tính các góc còn lại của hình bình hành ABCD trong hình 3.35

Đáp án chuẩn:

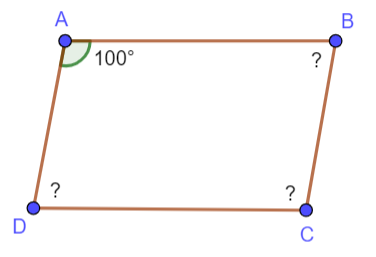
Bài 3.15. Cho hình bình hành ABCD. Gọi E, F lần lượt là trung điểm của các cạnh AB, CD. Chứng minh BF = DE

Đáp án chuẩn:

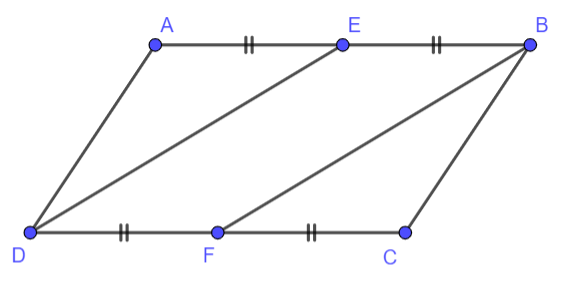
Tứ giác DEBF là hình bình hành (EB // DF ; EB = DF).

=>DE = BF (đpcm)

Bài 3.16. Trong mỗi trường hợp sau đây, tứ giác nào là hình bình hành, tứ giác nào không là hình bình hành, vì sao?

Đáp án chuẩn:

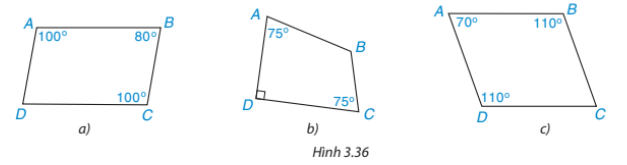
+) Hình 3.36 a là hình bình hành. Vì: ; 

+) Hình 3.36 b không phải hình bình hành. Vì :

+) Hình 3.36 c là hình bình hành. Vì:;

Bài 3.17.  Cho hình bình hành ABCD. Gọi E, F lần lượt là trung điểm của các cạnh AB, CD. Chứng minh rằng: 

1. Hai tứ giác AEFD, AECF là những hình bình hành
2. EF = AD; AF=EC

Đáp án chuẩn:

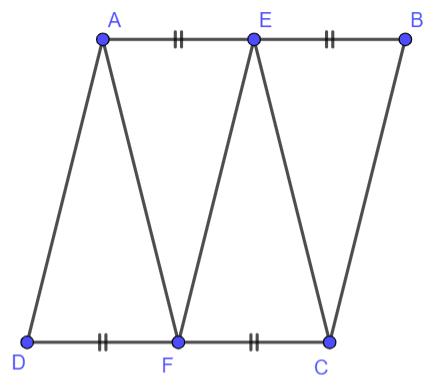
a) Xét tứ giác AEFD có: AE // DF và AE = DF => AEFD là hình bình hành.

+) Xét tứ giác AECF có: AE // CF và AE = CF => AECF là hình bình hành.

b) AEFD là hình bình hành => EF = AD 

+) AECF là hình bình hành => AF = EC 

Bài 3.18. Gọi O là giao điểm của hai đường chéo của hình bình hành ABCD. Một đường thẳng đi qua O lần lượt cắt AB, CD của hình bình hành tại hai điểm M,N. Chứng minh = . Từ đó suy ra tứ giác MBND là hình bình hành.

Đáp án chuẩn:

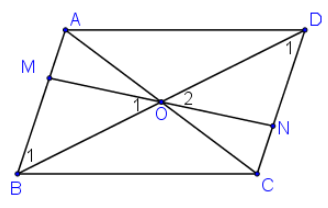
+) Xét và có: OA = OC; ;

=> =  

+) Ta có: BM // DN và BM = DN => tứ giác MBND là hình bình hành