BÀI TẬP CUỐI CHƯƠNG III

I. TRẮC NGHIỆM

Câu 3.39. Trong các khẳng định sau, khẳng định nào đúng?

1. Không có tứ giác nào mà không có góc tù

2. Nếu từ giác có ba góc nhọn thì góc còn lại là góc tù

3. Nếu tứ giác có hai góc tù thì hai góc còn lại phải nhọn

4. Không có tứ giác nào có 3 góc tù

Đáp án chuẩn:

B

Câu 3.40. Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?

1. Tứ giác có hai đường chéo bằng nhau là hình bình hành

2. Tứ giác có hai cặp cạnh bằng nhau là hình bình hành

3. Tứ giác có ba góc vuông là hình chữ nhật

4. Tứ giác có bốn cặp cạnh bằng nhau là hình thoi

Đáp án chuẩn:

A, D: Sai

B, C: Đúng

Câu 3.41. Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?

a) Tứ giác có hai cạnh đối nào cũng bằng nhau là hình bình hành. Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật

b) Tứ giác có hai cạnh đối nào cũng bằng nhau là hình bình hành

c) Tứ giác có hai cạnh song song và hai đường chéo bằng nhau là hidnh thang cân

d) Tứ giác có hai cạnh song song và hai cạnh còn lại bằng nhau là hình bình hành

Đáp án chuẩn:

a, b, c: Đúng

d: Sai

II. TỰ LUẬN

Bài 3.42. Chứng minh rằng nếu tứ giác có hai đường chéo bằng nhau và một cặp cạnh đối bằng nhau thì tứ giác đó là một hình thang cân.

Đáp án chuẩn:

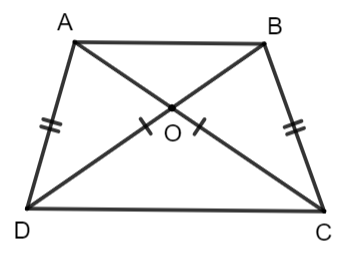
Chứng minh : 

ODC cân tại O (1)

 OAB cân tại O (2) 

Mặt khác (đối đỉnh) (3)

Từ (1), (2), (3) AB // DC (so le trong) ABCD là hình thang

Lại có AC = BD nên ABCD là hình thang cân.

Bài 3.43. Cho hình bình hành ABCD. Lấy điểm P trên tia AB sao cho AP = 2 AB 

1. Tứ giác BPCD có phải là hình bình hành không? Tại sao?
2. Khi tam giác ABD vuông cân tại A, hãy tính số đo các góc của tứ giác BPCD

Đáp án chuẩn:

a) BPCD là hình bình hành vì BP // CD, BP = CD 

b) ,

Bài 3.44. Cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC còn P, N lần lượt là chân đường vuông góc hạ từ M xuống CA, AB (H.3.59)

1. Chứng minh hai tam giác vuông CMP và MBN bằng nhau
2. Chứng minh tứ giác APMN là một hình chữ nhật

Từ đó suy ra N là trung điểm của AB, P là trung điểm của AC

1. Lấy điểm Q sao cho P là trung điểm MQ, chứng minh rằng tứ giác AMCQ là một hình thoi.
2. Nếu AB = AC, tức là tam giác ABC vuông cân tại A thì tứ giác AMCQ là hình vuông không? Vì sao?

Đáp án chuẩn:

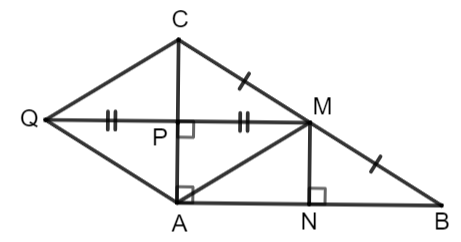
a) CMP = MBN (ch – gn)

b) Tứ giác APMN có 3 góc vuông nên là hình chữ nhật MP = AN ; AP = MN

Ta có CMP = MBN MP = BN ; CP = MN

AN = BN ; AP = CP

N là trung điểm của AB ; P là trung điểm của AC.

c) Chứng minh AMCQ là hình bình hành mà MQ AC nên AMCQ là hình thoi

d) Nếu AB = AC thì tam giác ABC vuông cân tại A thì suy ra . Lại có  nên AMCQ là hình vuông.

Bài 3.45. Cho tam giác ABC cân tại A; M là một điểm thuộc đường thẳng BC, B ở giữa M và C. Gọi E và K lần lượt là chân đường vuông góc hạ từ M và từ B xuống AC, còn N là chân đường vuông góc hạ từ B xuống ME và từ M xuống AB. (H.3.61)

Chứng minh rằng:

1. Tứ giác BKEN là hình chữ nhật
2. BK bằng hiệu khoảng cách từ M đến AC và đến AB (dù M thay đổi trên đường thẳng BC miễn là B nằm giữa M và C) lúc là BK = ME = MD.

Đáp án chuẩn:

a) Xét tứ giác BKEN có 3 góc vuông => BKEN là hình chữ nhật

b) NBM = DBM (ch – gn) MN = MD

Ta có ME là khoảng cách từ M đến đường thẳng AC, MN = MD là khoảng cách từ M đến đường thẳng AB, ME – MD = ME – MN = NE = BK (đpcm)