TRẮC NGHIỆM

Bài 3.39 – 3.41. Trang 74 sgk toán 8 tập 1

Đáp án:

Câu 3.39. Trang 74 sgk toán 8 tập 1

Đáp án B. 

Câu 3.40. Trang 74 sgk toán 8 tập 1

1. Sai. Vì tứ giác có hai đường chéo bằng nhau là hình thang cân.
2. Đúng. 
3. Đúng. 
4. Sai. Vì tứ giác có bốn cạnh bằng nhau là hình thoi.

Câu 3.41. Trang 74 sgk toán 8 tập 1

1. Đúng. 
2. Đúng. 
3. Đúng. 
4. Sai. Vì hai cạnh còn lại bằng nhau nhưng không song song thì không là hình bình hành.

TỰ LUẬN

Bài 3.42. Trang 74 sgk toán 8 tập 1

Chứng minh rằng nếu tứ giác có hai đường chéo bằng nhau và một cặp cạnh đối bằng nhau thì tứ giác đó là một hình thang cân.

Đáp án:

Xét ∆BCD và ∆ADC có : chung cạnh DC , BD = AC , BC = AD

∆BCD = ∆ADC (c.c.c) 

$\widehat{BDC} = \widehat{ACD} \Rightarrow ∆OCD$ cân tại O (1)

Chứng minh tương tự, ta có :  ∆OAB cân tại O (2) 

$\widehat{COD} = \widehat{BOA}$ (đối đỉnh) (3)

Từ (1), (2), (3) suy ra $\widehat{OCD} = \widehat{ODC} = \widehat{OAB} = \widehat{OBA}$

AB // DC (so le trong)

ABCD là hình thang 

Mà AC = BD (gt) $\Rightarrow ABCD$ là hình thang cân

Bài 3.43. Trang 74 sgk toán 8 tập 1

Cho hình bình hành ABCD. Lấy điểm P trên tia AB sao cho AP = 2 AB…

Đáp án:

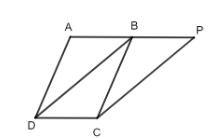
a) ABCD là hình bình hành nên $AB // CD \Rightarrow  BP // CD$

$AP = 2AB \Rightarrow BP = AB = CD \Rightarrow BPCD$ là hình bình hành.

b) ΔABD vuông cân tại A $\Rightarrow \widehat{ABD} = \widehat{ADB} = 45^{\circ}$

$\Rightarrow \widehat{DBP} = \widehat{DCP} = 135^{\circ}; \widehat{BDC} = \widehat{BPC} = 45^{\circ}$

Bài 3.44. Trang 75 sgk toán 8 tập 1

Cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC còn P, N lần lượt là chân đường vuông góc hạ từ M xuống CA, AB (H.3.59)…

Đáp án:

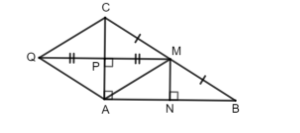
a) MP // BA ( cùng  AC ) $\Rightarrow \widehat{CMP} = \widehat{NBM}$ (đồng vị)

Xét hai tam giác vuông ∆MNB và ∆CPM có :

MB = MC

$\widehat{NBM} = \widehat{CMP}$ 

$\Rightarrow ∆MNB = ∆CPM (ch – gn)$

b) Xét tứ giác ANMP có: $\widehat{PAN} = \widehat{MPA} = \widehat{MNA} =  90^{\circ}$

$\Rightarrow ANMP$ là hình chữ nhật $\Rightarrow MN = AP ; AN= MP (1)$

∆MNB = ∆CPM (cmt)

$\Rightarrow MN = CP ; BN = MP (2)$

(1) và (2) $\Rightarrow AP = CP; AN = BN$

$\Rightarrow$ P là trung điểm của AC; N là trung điểm của AB (đpcm)

c) Tứ giác AQCM có hai đường chéo AC và QM cắt nhau tại P là trung điểm mỗi đường

$\Rightarrow AQCM$ là hình bình hành.

$AC\perp QM \Rightarrow AQCM$ là hình thoi

d) Δ ABC vuông cân tại A $\Rightarrow \widehat{ACB} = 45^{\circ}$

 $\Rightarrow \widehat{MCQ} = 90^{\circ}$ 

Hình thoi AQCM có $\widehat{MCQ} = 90^{\circ} \Rightarrow AQCM$ là hình vuông.

Bài 3.45. Trang 75 sgk toán 8 tập 1

Cho tam giác ABC cân tại A; M là một điểm thuộc đường thẳng BC, B ở giữa M và C. Gọi E và K lần lượt là chân đường vuông góc hạ từ M ….

Đáp án:

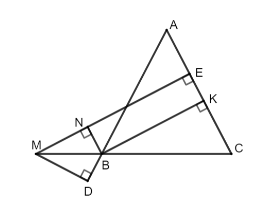
a) Xét tứ giác BNEK có $\widehat{KEN} = \widehat{BKE} = \widehat{BNE} = 90^{\circ}$

$\Rightarrow BNEK$ là hình chữ nhật

b) $\widehat{MBD} = \widehat{ABC}$ ( hai góc đối đỉnh)

$\widehat{NBM} = \widehat{ACB}$ (hai góc đồng vị)

$\widehat{ABC} = \widehat{ACB}$ ( Δ ABC cân tại A)

$\widehat{MBD} = \widehat{ABC} = \widehat{ACB} = \widehat{NBM}$

Xét hai Δ vuông MBD và MBN có: chung cạnh MB, $\widehat{MBD} = \widehat{MBN}$ 

∆MBD = ∆MBN (ch – gn) $\Rightarrow MD = MN$

$BK = NE = ME – MN = ME – MD (đpcm)$