TRẮC NGHIỆM

Bài 2.28 – 2.31. Trang 47 sgk toán 8 tập 1

Đáp án:

Giải chi tiết:

Câu 2.28:

$x^2 - 9x + 8 = x^2 - 8x – x + 8 = (x^2 - 8x) - (x – 8)$ 

= $x(x – 8) – (x – 8) = (x - 1)(x - 8)$

Câu 2.29:

$A^2 – B^2 = (A-B)(A+B)$.

Câu 2.30:

$25x^2 + 20xy + 4y^2 = (5x)^2 + 2.5x.2y + (2y)^2 = (5x + 2y)^2$ 

Câu 2.31:

$A = (2x + 1)^3 - 6x(2x + 1)$

= $8x^3 +12x^2 + 6x + 1 - 12x^2 - 6x = 8x^3 + 1$

TỰ LUẬN

Bài 2.32. Trang 47 sgk toán 8 tập 1

Tính nhanh giá trị của các biểu thức:

Đáp án:

a) $x^2 - 4x + 4 = (x – 2)^2$

Tại $x = 102$ ta có : $(102-2)^2 = 100^2 = 10 000$.

b) $x^3 + 3x^2 + 3x + 1 = (x +1)^3$

Tại $x = 999$ ta có : $(999 + 1)^3 = 1 000^3 = 1 000 000 000$

Bài 2.33. Trang 47 sgk toán 8 tập 1

Rút gọn các biểu thức:

a) $(2x - 5y)(2x + 5y) + (2x + 5y)^2$

b) $(x + 2y)(x^2 - 2xy + 4y^2) + (2x - y)(4x^2 + 2xy + y^2)$

Đáp án:

a) $(2x - 5y)(2x + 5y) + (2x + 5y)^2$

= $4x^2 - 25y^2 + 4x^2 + 20xy + 25y^2 = 8x^2 + 20xy$

b) $(x + 2y)(x^2 - 2xy + 4y^2) + (2x - y)(4x^2 + 2xy + y^2)$

= $x^3 + (2y)^3 + (2x)^3 – y^3 = x^3 + 8y^3 + 8x^3 – y^3 = 9x^3 + 7y^3$

Bài 2.34. Trang 47 sgk toán 8 tập 1

Phân tích đa thức sau thành nhân tử:

$6x^2 - 24y^2$  

$64x^3 - 27y^3$

$x^4 - 2x^3 + x^2$

$(x – y)^3 + 8y^3$

Đáp án:

a) $6x^2 - 24y^2 = 6.(x^2 - 4y^2) = 6(x-2y)(x+2y)$ 

b) $(4x)^3 – (3y)^3 = (4x - 3y)[(4x)^2 + 4x.3y + (3y)^2]$

= $(4x - 3y)(16x^2 + 12xy + 9y^2)$ 

c) $x^4 - 2x^3 + x^2 = x^2.(x^2 - 2x + 1) = x^2.(x – 1)^2$

d) $(x – y)^3 + (2y)^3 = (x – y + 2y)[(x – y)^2 – (x – y).2y + (2y)^2]$ 

= $(x + y)(x^2 - 2xy + y^2 - 2xy + 2y^2 + 4y^2)$

= $(x + y)(x^2 + 7y^2 - 4xy)$ 

Bài 2.35. Trang 47 sgk toán 8 tập 1

Sử dụng hình 2.3, bằng cách tính diện tích hình vuông ABCD theo hai cách…

Đáp án:

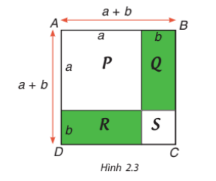
Cách 1 :

$S_{ABCD} = (a + b)^2$

Cách 2 : 

$S_{ABCD} = S_{P} + S_{R} + S_{Q} + S_{S}$

= $a^2 + ab + ab + b^2 = a^2 + 2ab + b^2$ 

Do đó $(a + b)^2 = a^2 + 2ab + b^2$.