HÌNH THOI

HĐ1. Trang 68 sgk toán 8 tập 1

Cho hình thoi ABCD có hai đường chéo AC, BD cắt nhau tại O (H.3.48)

Đáp án:

a) $AB = AD\Rightarrow ΔAB$  cân tại A

b) OB = OD ( ABCD là hình thoi nên cũng là hình bình hành)

Xét ΔBOA và ΔDOA :

AB = AD

Chung cạnh AO

BO = DO 

$\Rightarrow ΔBOA = ΔDOA (c.c.c) \Rightarrow \widehat{A_1} = \widehat {A_2} \Rightarrow AC$ là đường phân giác của $\widehat{A}$

Δ ABD cân suy ra $AC\perp BD$

Luyện tập 1. Trang 69 sgk toán 8 tập 1

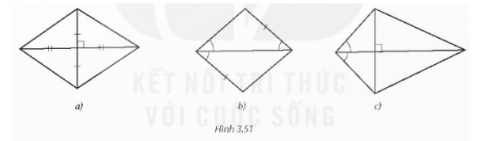
Trong Hình 3.51, hình nào là hình thoi? Vì sao?

Đáp án:

Hình a là hình thoi vì có hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.

Hình b là hình thoi vì có một cặp cạnh đối song song và bằng nhau và có một đường chéo là đường phân giác của một góc.

Hình c không là hình thoi vì bốn cạnh không bằng nhau.

HÌNH VUÔNG

HĐ2. Trang 70 sgk toán 8 tập 1

Hãy giải thích tại sao hai đường chéo của hình vuông bằng nhau và vuông góc với nhau.

Đáp án:

Hình vuông cũng là hình chữ nhật $\Rightarrow$ hai đường chéo bằng nhau

Hình vuông cũng là hình thoi $\Rightarrow$ hai đường chéo vuông góc với nhau

Luyện tập 2. Trang 71 sgk toán 8 tập 1

Với mỗi hình dưới đây, ta dùng dấu hiệu nhận biết nào để khẳng định đó là hình vuông?

Đáp án:

a) AC và BD cắt nhau tại trung điểm mỗi đường và có hai cạnh kề AB = BC.

b) FH và EG cắt nhau tại trung điểm mỗi đường; $\widehat A = 90^{\circ}$; FH là đường phân giác.

c) $IK\perp JL$ tại Q là trung điểm của mỗi đường.

GIẢI BÀI TẬP CUỐI SGK

Bài 3.29. Trang 71 sgk toán 8 tập 1

Tìm các hình thoi và hình vuông trong Hình 3.55

Đáp án:

b) EFGH là hình thoi vì $EG\perp FH$ tại trung điểm của mỗi đường.

c) MNPQ là hình vuông vì $MP\perp NQ$ và 

$\widehat{Q} = \widehat{M}=\widehat{N}=\widehat{P}= 90^{\circ}$

Bài 3.30. Trang 72 sgk toán 8 tập 1

Cho tam giác ABC, D là một điểm nằm giữa B và C. Qua D kẻ các đường thẳng song song với AB, AC, chúng cắt các cạnh AC, AB lần lượt tại E, F…

Đáp án:

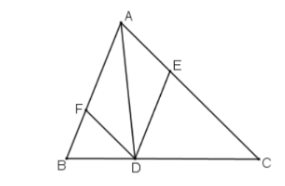
a) $DF // AE, DE // AF (gt) \Rightarrow AFDE$ là hình bình hành

b) Hình bình hành AFDE là hình thoi khi AD là tia phân giác của $\widehat{A}$. 

Mà ΔABC cân tại A $\Rightarrow AD$ đồng thời là trung tuyến $\Rightarrow$ D là trung điểm của BC.

c) Nếu ΔABC vuông tại A thì AFDE là hình chữ nhật .

d) D là trung điểm cạnh BC thì AFDE là hình vuông.

Bài 3.31. Trang 72 sgk toán 8 tập 1

Chứng minh rằng các trung điểm của bốn cạnh trong một hình chữ nhật là các đỉnh của một hình thoi.

Đáp án:

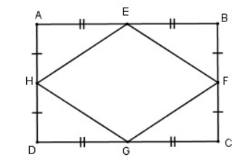
Xét ∆AHE và ∆BFE có : 

AH = BF

$\widehat{EAH} = \widehat {FBE} = 90^{\circ}$

AE = BE 

$\Rightarrow ∆AHE = ∆BFE (c.g.c)$

$\Rightarrow HE = FE (1)$

Chứng minh tương tự, ta có:

$∆AEH = ∆DGH (c.g.c) \Rightarrow HE = HG (2)$

$∆DHG = ∆CFG (c.g.c) \Rightarrow HG = GF (3)$

Từ (1), (2) và (3) $\Rightarrow HE = EF = HG = GF \Rightarrow EHGF$ là hình thoi.

Bài 3.32. Trang 72 sgk toán 8 tập 1

Chứng minh rằng các trung điểm của bốn cạnh trong một hình thoi là các đỉnh của một hình chữ nhật.

Đáp án:

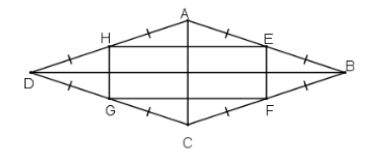
Xét ∆DHG và ∆BEF có : 

DH = BE

$\widehat{HDG} = \widehat{EBF}$ 

DG = BF

$\Rightarrow ∆DHG = ∆BEF (c.g.c)$

$\Rightarrow HG = EF (1)$

Chứng minh tương tự, ta có:

$∆AHE = ∆CGF (c.g.c) \Rightarrow HE = GF (2)$

Từ (1) và (2) $\Rightarrow HGFE$ là hình bình hành. (3)

Gọi O là giao điểm của AC và BD 

 ∆OCD = ∆OAD = ∆OCB = ∆OAB

$\Rightarrow OG = OH = OF = OE (4)$

Từ (3) và (4) $\Rightarrow HGFE$ là hình chữ nhật

Bài 3.33. Trang 72 sgk toán 8 tập 1

Cho hình chữ nhật ABCD có chu vi bằng 36 cm. Gọi M là trung điểm của cạnh BC…

Đáp án:

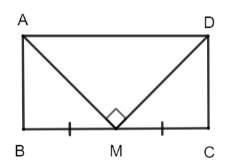
Xét ∆MBA và ∆MCD :

BM = CM

$\widehat{B} = \widehat{C} = 90^{\circ}$

AB = DC

$\Rightarrow ∆MBA = ∆MCD (c.g.c)$

$\Rightarrow AM = MD$

Có $\widehat{AMD} = 90^{\circ}  \Rightarrow \widehat{CMD} = \widehat{BMA} = 45^{\circ}$

$\Rightarrow ∆CMD$ vuông cân tại C; ∆BAM vuông cân tại B

$CD = MC = BM =AB$

$AB + BC = 36 : 2= 18 (cm)$

$\Rightarrow AB = CD = 18 : 3 = 6 (cm)$

$\Rightarrow BC = AD = 6 . 2 = 12 (cm)$