ĐOẠN THẲNG TỈ LỆ

HĐ1. Trang 77 sgk toán 8 tập 1

Hãy tìm độ dài của hai đoạn thẳng AB và CD nếu chọn đoạn MN làm đơn vị độ dài…

Đáp án:

$AB = 2.MN ; CD = 6.MN$

$\Rightarrow \frac{AB}{CD} = \frac{2MN}{6MN} = \frac{1}{3}$ 

HĐ2. Trang 77 sgk toán 8 tập 1

Dùng thước thẳng, đo độ dài hai đoạn AB và CD (đơn vị: cm)…

Đáp án:

$AB = 3 cm; CD = 9 cm \Rightarrow \frac{AB}{CD} = \frac{3}{9} = \frac{1}{3}$ 

HĐ3. Trang 77 sgk toán 8 tập 1

So sánh tỉ số tìm được trong hai hoạt động trên

Đáp án:

Tỉ số $\frac{AB}{CD}$ ở HĐ 1 và HĐ 2 bằng nhau và đều bằng $\frac{1}{3}$ .

Luyện tập 1. Trang 77 sgk toán 8 tập 1

Tìm tỉ số của các cặp đoạn thẳng có độ dài như sau:

a) MN = 3 cm và PQ = 9 cm

b) EF = 25 cm và HK = 10 dm

Đáp án:

a)  $\frac{MN}{PQ} = \frac{3}{9} = \frac{1}{3}$

b) $EF = 25 cm = 2,5 dm; \frac{EF}{HK} = \frac{2,5}{10} = \frac{1}{4}$ 

Luyện tập 2. Trang 78 sgk toán 8 tập 1

Cho tam giác ABC và một điểm B' nằm trên cạnh AB. Qua điểm B', ta vẽ một đường thẳng song song với BC, cắt AC tại C' (H.4.4)…

Đáp án: 

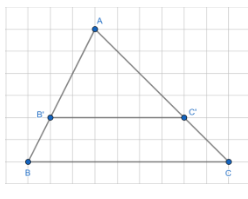
a) $\frac{AB'}{AB} = \frac{AC'}{AC} = \frac{4}{6} = \frac{2}{3}$

b) $\frac{AB'}{B'B} = \frac{AC'}{C'C} = \frac{4}{2} = 2$ 

c) $\frac{B'B}{AB} = \frac{C'C}{AC} = \frac{2}{6} = \frac{1}{3}$  

ĐỊNH LÍ THALÈS TRONG TAM GIÁC

Luyện tập 3. Trang 79 sgk toán 8 tập 1

Tìm các độ dài x, y trong hình 4.6

Đáp án:

a) $\frac{AM}{MB} = \frac{AN}{NC} \Rightarrow \frac{6,5}{x} = \frac{4}{2}$

$\Rightarrow x = 6,5 . 2 : 4 = 3,25$

b) $EF // HQ$ ( do cùng$\perp PH$)

$\frac{PE}{PH} = \frac{PF}{FQ} \Rightarrow \frac{4y}{5} = {5 + 3,5}$

$y = 4 . 8,5 : 5 = 6,8$

HĐ 4. Trang 79 sgk toán 8 tập 1

Cho ΔABC có AB = 6 cm, AC = 9 cm. Trên cạnh AB lấy điểm B', trên cạnh AC lấy điểm C' sao cho AB' = 4 cm, AC' = 6 cm (H.4.7)…

Đáp án:

$\frac{AB'}{AB} = \frac{4}{6} = \frac{2}{3}$;

$\frac{AC'}{AC} = \frac{6}{9} = \frac{2}{3}$

$\Rightarrow \frac{AB'}{AB} = \frac{AC'}{AC}$

$\frac{AB'}{AB} = \frac{AC''}{AC} \Rightarrow \frac{4}{6} = \frac{AC''}{9}$

$\Rightarrow AC'' = 4 . 9 : 6 = 6 (cm)$

$AC’ = AC” = 6cm; C’≡ C” ; B’C’ // BC$

GIẢI BÀI TẬP CUỐI SGK

Bài 4.1. Trang 80 sgk toán 8 tập 1

Tìm độ dài x, y trong Hình 4.9 (làm tròn kết quả đến chữ số thập phân thứ nhất).

Đáp án:

a) $\frac{HP}{HQ} = \frac{KP}{KE} \Rightarrow \frac{6}{4} = \frac{8}{x}$

$\Rightarrow x = 4 . 8 : 6 ≈ 5,3$ (đvđd)

b) $\widehat{NMA} = \widehat{CBA}$ (hai góc đồng vị)

$\Rightarrow MN // BC$

$NC = AC – NA = 11 – 8 = 3$

$\frac{AM}{BM} = \frac{AN}{CN} \Rightarrow \frac{y}{6,5} = \frac{8}{3}$

$\Rightarrow y = 6,5 . 8 : 3 ≈ 17,3$ (đvđd)

Bài 4.2. Trang 80 sgk toán 8 tập 1

Tìm các cặp đường thẳng song song trong Hình 4.10 và giải thích vì sao chúng song song với nhau.

Đáp án:

a) $\frac{ME}{NE} = \frac{FM}{FP} = \frac{2}{3} \Rightarrow EF // MN$ 

b) $\frac{QM}{HM} = \frac{QE}{KE} = \frac{2}{3} \Rightarrow ME // HK$

$\frac{HF}{KF} = \frac{7}{6} \neq \frac{HM}{MQ} = \frac{3}{2}$

$\Rightarrow$ FM và KQ không song song với nhau

Bài 4.3. Trang 80 sgk toán 8 tập 1

Cho tam giác ABC, từ điểm D trên cạnh BC, kẻ đường thẳng song song với AB cắt AC tại F và kẻ đường thẳng song song với AC cắt AB tại E…

Đáp án:

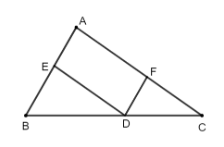
$ED // AC \Rightarrow \frac{AE}{AB} = \frac{CD}{BC}$

$FD // AB \Rightarrow  \frac{AF}{AC} = \frac{BD}{BC}$

$\Rightarrow \frac{AE}{AB} + \frac{AF}{AC} = \frac{CD}{BC} + \frac{BD}{BC}$

= $\frac{CD + BD}{BC} = \frac{BC}{BC} = 1$ (đpcm)

Bài 4.4. Trang 80 sgk toán 8 tập 1

Cho tam giác ABC có trọng tâm G. Vẽ đường thẳng d qua G và song song với AB, d cắt BC tại điểm M. Chứng minh rằng…

Đáp án:

Gọi D là trung điểm của cạnh BC.

Vì G là trọng tâm của tam giác ABC $\Rightarrow \frac{AG}{AD} = \frac{2}{3}$ 

Vì $MG // AB \Rightarrow \frac{AG}{AD} = \frac{BM}{BD} = \frac{2}{3}$

Vì D là trung điểm của cạnh $BC \Rightarrow \frac{BM}{BC} = \frac{BM}{2BD}$

= $\frac{2}{2.3} = \frac{1}{3}$ (đpcm)

Bài 4.5. Trang 80 sgk toán 8 tập 1

Để đo khoảng cách giữa hai vị trí B và E ở hai bên bờ sông, bác An chọn ba vị trí , F, C cùng nằm ở một bên bờ sông sao cho ba điểm C, E, B thẳng hàng,…

Đáp án:

AB // EF, áp dụng định lí Thalès, ta có:

$\frac{CF}{AF} = \frac{EC}{BE} \Rightarrow \frac{20}{40} = \frac{30}{BE}$

$\Rightarrow BE = 40.30 : 20 = 60 (m)$

Vậy $BE= 60 m$