Bài 3.9. Trang 56 sgk toán 8 tập 1

Tứ giác ABCD trong hình 3.25 có phải là hình thang không? Vì sao?

Đáp án:

Ta có: $\widehat{A}$ và $\widehat{D}$ bù nhau.

Gọi Ax là tia đối của tia AD thì: $\widehat{xAB} = \widehat{CDA}$  

$\Rightarrow AB // DC$ (hai góc đồng vị bằng nhau)

Vậy ABCD là hình thang.

Bài 3.10. Trang 56 sgk toán 8 tập 1

Cho hình thang cân ABCD (AB//CD) có AB = AD. Biết góc ABC…

Đáp án:

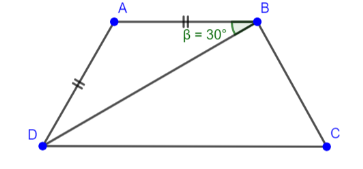
Ta có ∆ABD cân tại A  $\Rightarrow \widehat{ABD} = \widehat{ADB} = 30^{\circ}$.

Vì AB // CD nên $\widehat{ABD} = \widehat{ BDC} = 30^{\circ}$ (so le trong).

$\Rightarrow \widehat{ADC} = 60^{\circ}$.

Mà ABCD là hình thang cân nên $\widehat{BCD} = \widehat{ADC} = 60^{\circ}; \widehat{BAD} = \widehat{ABC} = 120^{\circ}$.

Bài 3.11. Trang 56 sgk toán 8 tập 1

Tính số đo các góc của tứ giác ABCD trong hình 3.26

Đáp án:

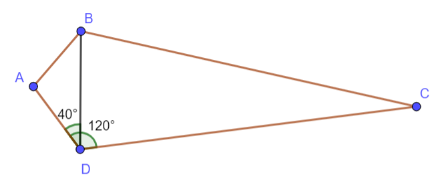
∆ABD cân tại A nên $\widehat{A} = 180^{\circ} – 40^{\circ} . 2 = 100^{\circ}$.

$\widehat{BDC} = 120^{\circ} -  40^{\circ} =  80^{\circ}$

∆CBD cân tại C nên $\widehat{C} = 180^{\circ} – 80^{\circ} . 2 = 20^{\circ}$

$\widehat{ABC} = \widehat{ABD} + \widehat{DBC} = 40^{\circ} + 80^{\circ} = 120^{\circ}$.

Bài 3.12. Trang 56 sgk toán 8 tập 1

Cho M là một điểm nằm trong tam giác đều ABC. Qua M kẻ các đường thẳng song song với BC, CA, AB lần lượt cắt AB, BD, CA, tại các điểm P, Q, R.

Đáp án:

a) Vì MR // AP nên APMR là hình thang

Có $\widehat{A} = \widehat{B} = \widehat{MPA}$ (do MP // CB) nên APMR là hình thang cân.

b) Chứng minh tương tự ta có các tứ giác CQMR và PMQB là những hình thang cân.

$\Rightarrow RP = MA, RQ = MC , QP = MB$ (hai đường chéo của hình thang cân). 

$P_{PQR} = RP + RQ + QP = MA + MB + MC$

c) ∆PQR làm tam giác đều ⬄ RP = RQ = QP ⬄ MB = BC = MA. 

Vậy M cách đều ba đỉnh A, B, C tức M là trọng tâm của tam giác đều ABC.