HÌNH THANG. HÌNH THANG CÂN

Luyện tập 1. Trang 53 sgk toán 8 tập 1

Tính các góc của hình thang cân ABCD (AB//CD)…

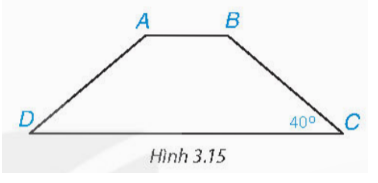
Đáp án:

Vì ABCD là hình thang cân (AB // CD) nên:

$\widehat{A} = \widehat{B}; \widehat{C} = \widehat{D} = 40^{\circ}$ 

Ta có: $\widehat{A} + \widehat{B} + \widehat{C} + \widehat{D} = 360^{\circ}$

$\Rightarrow 2\widehat{A} + 40^{\circ} + 40^{\circ} = 360^{\circ}$

$\Rightarrow \widehat{A}$ = $\widehat{B}$ = ($360^{\circ} - 40^{\circ} - 40^{\circ}$) : $2$ = $140^{\circ}$

TÍNH CHẤT CỦA HÌNH THANG

HĐ 1. Trang 53 sgk toán 8 tập 1

Cho hình thang cân ABCD, AB//CD và AB < CD (H3.16).

Đáp án:

a) Ta có AB // CD (gt) mà  $BI \perp CD (gt)$

$\Rightarrow BI ⊥ AB$. Suy ra $\widehat{IBA} = 90^{\circ}$.

Xét ∆AHI và ∆IBA có:

$\widehat{BAI} = \widehat{HIB}$ (so le trong)

AI chung

$\widehat{IHA} = \widehat{IBA} = 90^{\circ}$

$\Rightarrow$ ∆AHI = ∆IBA (g.c.g) => AH = BI

b) Xét ∆DHA và ∆CIB có:

$\widehat{D} = \widehat{C}$ (ABCD là hình thang cân)

AH = BI (theo a)

$\widehat{DHA} = \widehat{CIB} = 90^{\circ}$ 

$\Rightarrow$ ∆DHA=∆CIB (g.c.g)  

$\Rightarrow AD = BC$.

Luyện tập 2. Trang 53 sgk toán 8 tập 1

Cho tứ giác ABCD như hình 3.19. Biết rằng…

Đáp án:

Ta có: $\widehat{A} = \widehat{D_1}$ (gt) mà hai góc này ở vị trí đồng vị 

$\Rightarrow AB // DC$

Vậy tứ giác ABCD là hình thang.

Lại có $\widehat{A} = \widehat{B}$ (gt)

$\Rightarrow$ Hình thang ABCD cân

$\Rightarrow AD = BC$.

HĐ2. Trang 54 sgk toán 8 tập 1

Cho hình thang cân ABCD, kẻ hai đường chéo AC, BD (H3.19). Hãy chứng minh…

Đáp án:

Xét ∆ADC và ∆BCD có:

$AD = BC$

$\widehat{ADC} = \widehat{BCD}$ 

CD chung

$\Rightarrow ∆ADC=∆BCD (c.g.c) \Rightarrow AC = BD$.

Luyện tập 3. Trang 54 sgk toán 8 tập 1

Cho tam giác ABC cân tại A. Kẻ một đường thẳng ở song song với BC…

Đáp án:

a) Vì DE // BC nên tứ giác DECB là hình thang.

Lại có ∆ABC cân tại A => $\widehat{B} = \widehat{C}$

$\Rightarrow$  DECB là hình thang cân.

b) Xét ∆BCE và ∆CBD có:

Chung cạnh BC 

$\widehat{BCE} = \widehat{CBD}$

CE = BD 

$\Rightarrow  ∆BEC=∆CDB (c.g.c)$

$\Rightarrow BE = CD$

DẤU HIỆU NHẬN BIẾT

Vận dụng. Trang 55 sgk toán 8 tập 1

Hãy giải bài toán mở đầu.

Đáp án:

Ta có hình thang mới là: MN’M’N.

Ta có:

Hình thang AMND có: M’N’ là cạnh mới cắt (M'≡M;N'≡N); AD là cạnh bên.

Hình thang MBCN có: MN là cạnh mới cắt; BC là cạnh bên.

$\Rightarrow \widehat{AM'N} = \widehat{AMN} = \widehat{MNC}$ (so le trong)

$\Rightarrow$ Lật hình thang AN’M’D để ghép vào hình thang MBCN thì cạnh AD trùng với BC. 

Hình mới là MN’M’N có $\widehat{AM'N} = \widehat{MNC}$ 

Vậy  MN’M’N là hình thang cân.

GIẢI BÀI TẬP CUỐI SGK

Bài 3.4. Trang 55 sgk toán 8 tập 1

Hình thang trong hình 3.23 có là hình thang cân không? Vì sao?

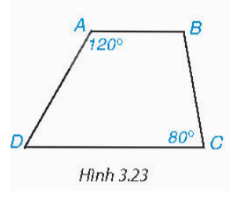
Đáp án:

Ta có : $\widehat{A} + \widehat{D} = 180^{\circ}$

$\Rightarrow \widehat{D} = 180^{\circ}  – 120^{\circ} = 60^{\circ}  ≠ \widehat{C} = 80^{\circ}$

$\Rightarrow$ Hình thang ABCD không phải là hình thang cân.

Bài 3.5. Trang 55 sgk toán 8 tập 1

Cho hình thang ABCD (AB//CD). Kẻ đường thẳng vuông góc với AC tại C và đường thẳng vuông góc với BC tại D….

Đáp án:

Gọi $AC \cap BD = H$

Xét hai tam giác vuông ∆EHC và ∆EHD có : 

EH chung;

EC = ED (gt) 

$\Rightarrow $ ∆EHC = ∆EHD (cạnh huyền – cạnh góc vuông)

$\Rightarrow CH = DH (1); \widehat{CEH} = \widehat{DEH}$

$\Rightarrow$ EH là phân giác của $\widehat{CED}$.

$\Rightarrow EH \perp CD \Rightarrow EH \perp AB (do AB // CD)$.

Gọi $EH \cap AB = K$

$∆EHC = ∆EHD \Rightarrow \widehat{EHC} = \widehat{EHD}$

$\Rightarrow \widehat{BHK} = \widehat{AHK}$ 

Xét tam giác vuông HKB và HKA có :

HK chung;

$\widehat{BHK} = \widehat{AHK}$ 

$\Rightarrow ∆HKB = ∆HKA$ (cạnh góc vuông-góc nhọn)

$\Rightarrow  HB = HA$ (2)

Từ (1) và (2) => AC = BD

Vậy ABCD là hình thang cân.

Bài 3.6. Trang 55 sgk toán 8 tập 1

Vẽ hình thang cân ABCD (AB//CD) biết đáy lớn CD dài 4cm, cạnh bên dài 2cm và đường chéo dài 3cm.

Đáp án:

Vẽ đáy lớn CD = 4 cm

Vẽ cung tròn tâm C bán kính 3 cm, cung tròn tâm D bán kính 2 cm, giao điểm của 2 cung tròn là A

Vẽ cung tròn tâm C bán kính 2 cm, cung tròn tâm D bán kính 3 cm, giao điểm của 2 cung tròn là B

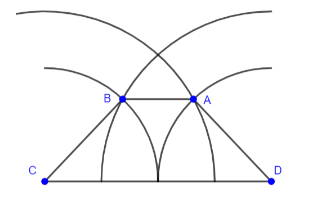
Bài 3.7. Trang 55 sgk toán 8 tập 1

Hai tia phân giác của hai góc A, B của hình thang cân ABCD (AB//CD) biết đáy lớn dài 4cm…

Đáp án:

Hình thang ABCD cân và AE, BE là phân giác BAD và ABC

$\widehat{E_1} = \widehat{B_2}; \widehat{E_3} = \widehat{A_2}$  (so le trong)

$\Rightarrow$ ∆ADE cân tại C, nên AD = ED (1).

$\Rightarrow $ ∆BCE cân tại C, nên BC = EC (2).

ABCD là hình thang cân nên AD = BC (3)

Từ (1),(2) và (3) suy ra: ED = EC

Bài 3.8. Trang 55 sgk toán 8 tập 1

Hình thang cân ABCD (AB//CD, AB//CD) có các đường thẳng AD, BC cắt nhau tại J….

Đáp án:

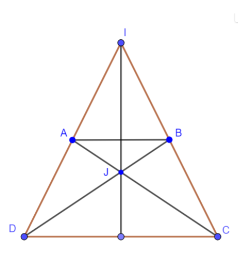
Xét ∆ADC và ∆BCD có:

AC = BD (đường chéo hình thang cân)

Chung cạnh CD

AD = BC (tính chất hình thang cân)

$\Rightarrow ∆ADC=∆BCD (c.c.c)$

$\Rightarrow \widehat{ACD} = \widehat{BDC}$ hay $\widehat{JCD} = \widehat{JDC}$

$\Rightarrow$ ∆JCD cân tại I

Do đó JD = JC (1)

∆ICD có hai góc ở đáy bằng nhau $\widehat{C} = \widehat{D}$ nên ∆ICD cân tại I.

$\Rightarrow  ID = IC (2)$

Từ (1) và (2) suy ra IJ là trung trực của CD.

Tương tự ta chứng minh được :  $JA = JB; IA = IB$

$\Rightarrow$ J và I cùng thuộc đường trung trực của đoạn thẳng AB

Do đó, IJ là đường trung trực của AB.