CHƯƠNG 3. TỨ GIÁC

BÀI 11. HÌNH THANG CÂN

1. HÌNH THANG. HÌNH THANG CÂN

Khái niệm hình thang và hình thang cân.

- Hai đường thẳng song song với nhau khi chúng không có điểm chung nào.

(hình 3.12)

Khái niệm:

Hình thang là tứ giác có hai cạnh đối song song.

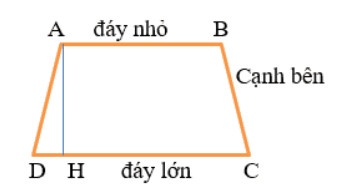
Hình tháng ABCD có:

+ Đáy nhỏ AB song song với đáy lớn CD.

+ Cạnh bên AD và BC.

+ Đường cao AH.

(hình 3.13)

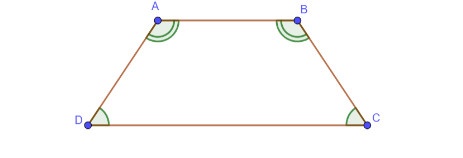
- Nhận xét: Hình thang ABCD có: AB // CD.

+ A=B

+ C=D

Vì A và B là hai góc kề cùng một đáy nhỏ AB nên hình thang ABCD là hình thang cân.

Định nghĩa:

Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.

Ví dụ 1.

Vì ABCD là hình thang (AB // CD) nên:

D=A1 (đồng vị).

Do DAB+A1=180o (hai góc kề bù)

Suy ra: D+DAB=180o.

Luyện tập 1

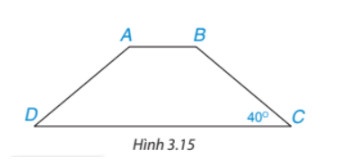
Vì ABCD là hình thang cân (AB // CD) nên:

C=D=40o 

A=B 

Ta có: A+B+C+D=360o

=> 2A+40o+40o=360o

=> A=B=360o-40o-40o2=140o

2. TÍNH CHẤT CỦA HÌNH THANG CÂN

Tính chất về cạnh bên của hình thang cân.

HĐ1:

1. a) Ta có AB // CD (gt) mà BI⊥CD (gt)

=> BI⊥AB. Suy ra ABI=90o.

∆AHI vuông tại H, ∆IBA vuông tại B

Xét ∆AHI và ∆IBA có:

BAI=HIA (so le trong)

AI chung

=> ∆IBA=∆AHI (cạnh huyền  - góc nhọn)

=> AH = BI 

1. b) Vì ABCD là hình thang cân => C=D (1)

• ∆AHD vuông tại H có DAH+D=90o (2)
• ∆BIC vuông tại I có CBI+C=90o (3)

Từ (1)(2)(3) => DAH=CBI

Xét ∆AHD và ∆BIC có:

AH=BI (câu a)

DAH=CBI (chứng minh trên)

=> ∆AHD=∆BIC (cạnh góc vuông – góc nhọn kề)

=> AD=BC

Định lí 1

Trong hình thang cân, hai cạnh bên bằng nhau.

Luyện tập 2

Ta có: D1=A (gt) mà hai góc này ở vị trí đồng vị, nên suy ra: DC // AB.

Vậy tứ giác ABCD là hình thang.

Lại có A=B => hình thang ABCD cân.

=> AD = BC.

Tính chất về đường chéo của hình thang cân.

HĐ2:

Xét ∆ACD và ∆BDC có:

CD chung

AD = BC

ADC=BCD 

=> ∆ACD=∆BDC (c.g.c)

=> AC = BD.

Định lí 2

Trong hình thang cân, hai đường chéo bằng nhau.

Luyện tập 3

1. a) Vì DE // BC nên tứ giác DECB là hình thang.

Lại có ∆ABC cân tại A => B=C

Suy ra hình thang DECB có hai góc kề 1 đáy bằng nhau nên là hình thang cân.

1. b) Vì DECB là hình thang cân (cmt) nên theo định lí 2 ta có:

BE=CD (hai đường chéo hình thang cân bằng nhau)

3. DẤU HIỆU NHẬN BIẾT

Dấu hiệu nhận biết hình thang cân.

Định lí 3:

Nếu một hình thang có hai đường chéo bằng nhau thì hình thang đó là hình thang cân.

Ví dụ 2: (SGK – tr.54).

Hướng dẫn giải (SGK – tr.54).

Thực hành

1. a) 
2. b) Hình thag ABCD là hình thang cân, vì theo định lí 3: Hình thang có 2 đường chéo bằng nhau là hình thang cân.

Vận dụng

+ Để ghép hai nửa hình thang cân ban đầu thành một hình thang cân mới, cần lật ngược một nửa rồi ghép với nửa kia sao cho hai cạnh bên được ghép khít nhau, nửa AMND trở thành CM'N'B.

+ Chỗ ghép ở B và C tạo thành đường thẳng, vì B+CBN'=A+D=180o 

+ Chỗ ghép ở C và M' tạo thành đường thẳng vì C+BCM'=C+DAM=D+A=180o.

+ Có N'M'C=NMA và NMA=MNM' (so le trong) => Hai góc ở đáy NM' của hình thang MN'M'N bằng nhau. 

Vậy hình thang đó cân.