Bài tập file word Toán 8 Kết nối bài 11: Hình thang cân
Bài tập và câu hỏi tự luận luyện tập ôn tập bài 11: Hình thang cân. Bộ câu hỏi bài tập mở rộng có 4 mức độ: Thông hiểu, nhận biết, vận dụng và vận dụng cao. Phần tự luận này sẽ giúp học sinh hiểu sâu, sát hơn về môn học Toán 8 Kết nối tri thức. Kéo xuống để tham khảo thêm
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
Nội dung quan tâm khác
Thêm kiến thức môn học
Từ khóa tìm kiếm: Bài tập luyện tập Toán 8 kết nối, luyện tập toán 8 kết nối bài 11, luyện tập bài 11: Hình thang cân, luyện tập toán 8 bài Hình thang cân

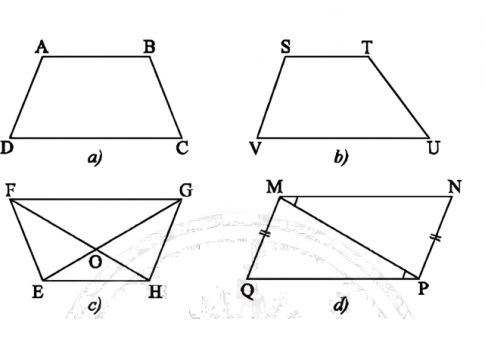
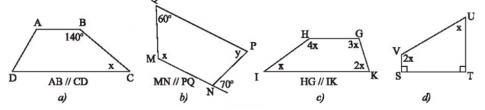
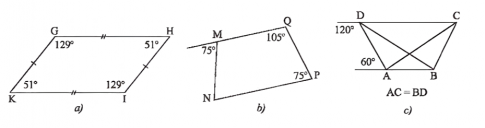
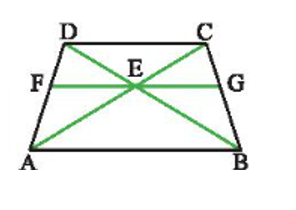
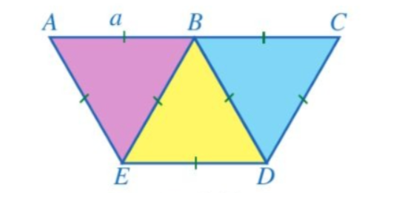


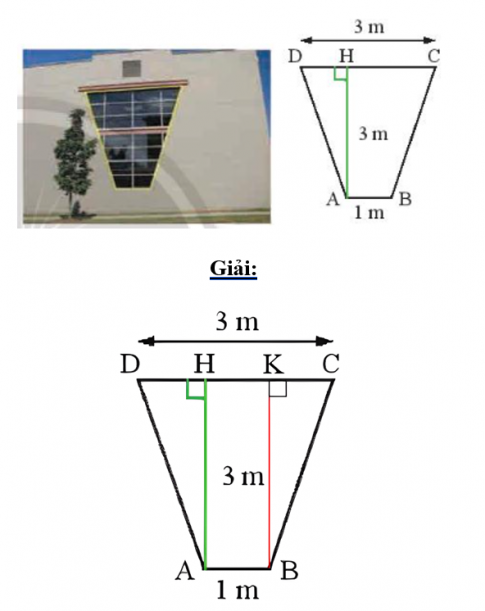
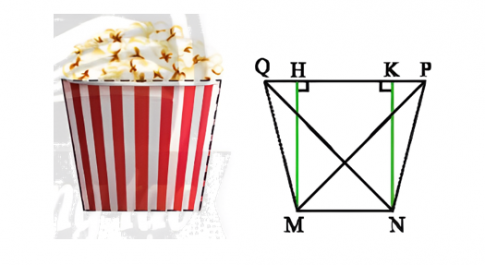
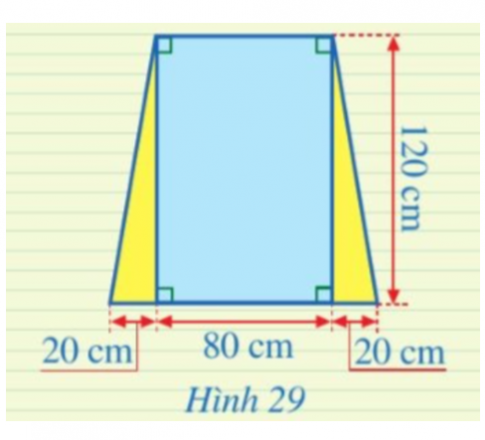
Bình luận