Bài tập file word mức độ vận dụng bài 11: Hình thang cân
3. VẬN DỤNG (5 câu)
Câu 1: Một mặt tường của chân tháp cột cờ Hà Nội có dạng hình thang cân ABCD (Hình vẽ). Cho biết $\widehat{D}=\widehat{C}=75^{\circ}$. Tìm số đo $\widehat{A}$ và $\widehat{B}$

Câu 2: Tứ giác EFGH có các góc cho như Hình vẽ

Câu 3. Một khung cửa sổ hình thang cân có chiều cao 3m, hai đáy là 3m và 1m (Hình 9). Tìm độ dài hai cạnh bên và hai đường chéo.
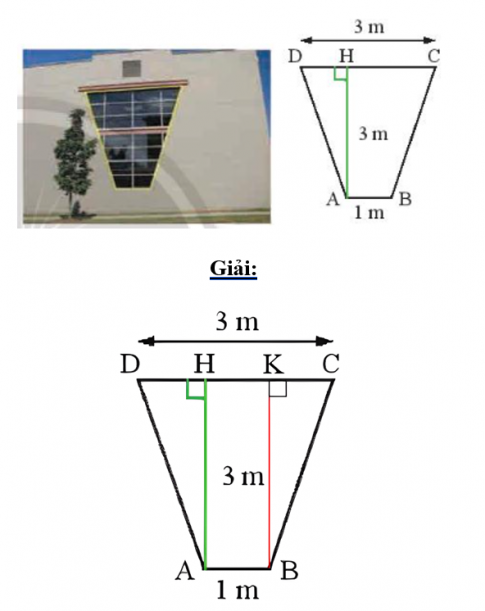
Bài 4. Mặt cắt của một li giấy đựng bỏng ngô có dạng hình thang cân MNPQ (Hình 13) với hai đáy MN = 6 cm, PQ = 10 cm và độ dài hai đường chéo $MN=NQ=8\sqrt{2}$ cm. Tính độ dài đường cao và cạnh bên của hình thang.
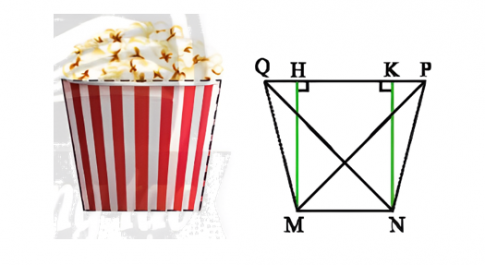
Câu 5: Một ô cửa số có dạng hình chữ nhật với chiêu dài là 120 cm và chiêu rộng là 80 cm. Người ta mở rộng ô cửa số đó bằng cách tăng độ dài cạnh dưới về hai bên, mỗi bên 20 cm (mô tả ở Hình 29). Sau khi mở rộng thì ô cửa số đó có dạng hình gì? Tính diện tích của ô cửa số đó sau khi mở rộng.
Câu 1:
Hình thang ABCD (AB // CD) có: $\widehat{D}= \widehat{C}=75^{\circ}$
suy ra $\widehat{A}= \widehat{B}=180^{\circ}-75^{\circ}=105^{\circ}$
Câu 2:
a) Ta có:
$\widehat{E}+ \widehat{F}=95^{\circ}+85^{\circ}=180^{\circ}$ hay $\widehat{E}$ và $\widehat{F}$ là hai góc bù nhau
Mà hai góc ở vị trí trong cùng phía
suy ra EH // FG
Do đó EFGH là hình thang (DHNB)
b) Hình thang EFGH (EH // FG) có:
$\widehat{H}=180^{\circ}-\widehat{G}=180^{\circ}-27^{\circ}=153^{\circ}$
Câu 3.
Kẻ BK vuông góc với CD ta có: HK = AB, DH = CK = (3 - 1) : 2 = 1(m)
Cho tam giác AHD vuông tại H ta có:
$AD^{2}=AH^{2}+DH^{2}$ (định lí Pythagore)
$3^{2}+1^{2}=10$
Do đó: $AD=BC=\sqrt{10}$ (m)
Xét tam giác AHC vuông tại H ta có:
$AC^{2}=AH^{2}+CH^{2}$ (định lí Pythagore)
$3^{2}+2^{2}=\sqrt{13}$ (m)
Do đó AC = $\sqrt{13}$ (m)
Suy ra AC=BD=$\sqrt{13}$ (m)
Bài 4.
Ta có QH = PK = (10 - 6) : 2 = 2(cm)
Áp dụng định lí Pythagore cho tam giác MPH vuông tại H ta có:
$MP^{2}=MH^{2}+PH^{2}$ suy ra $MH^{2}=MP^{2}-PH^{2}=128-64=64$ do đó MH = 8 cm
Xét tam giác MHQ vuông tại H ta có:
$MQ^{2}=MH^{2}+QH^{2}=64-4=60$
do đó MH = $2\sqrt{15}$ (cm)
Vậy độ dài đường cao là 8 cm, độ dài cạnh bên là $2\sqrt{15}$ cm
Câu 5:
Sau khi mở rộng thì ô cửa số đó có dạng hình thang cân.
Diện tích của ô cửa số đó sau khi mở rộng: $120.80+2.\frac{1}{2}.20.120=1200(cm^{2})$

Bình luận