Bài tập file word mức độ thông hiểu bài 11: Hình thang cân
2. THÔNG HIỂU (5 câu)
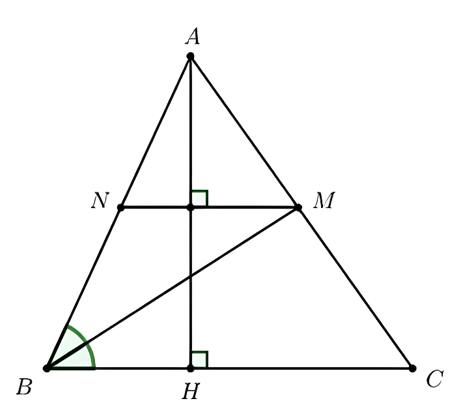
Câu 1. Cho tam giác nhọn ABC có AH là đường cao. Tia phân giác của góc B cắt AC tại M. Từ M kẻ đường thẳng vuông góc với AH cắt AB tại N.
a) Chứng minh rằng tứ giác BCMN là hình thang.
b) Chứng mình rằng BN = MN.
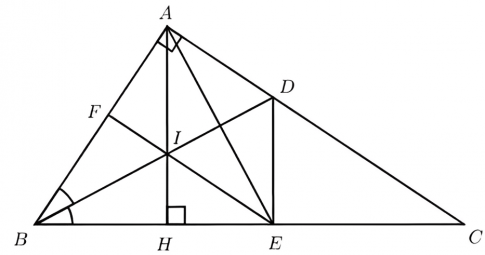
Câu 3: Cho tam giác ABC vuông tại A (AB < AC). Tia phân giác của góc B cắt AC tại D. Trên BC lấy điểm E sao cho BE = BA.
a) Chứng minh rằng: ΔABD=ΔEBD
b) Kẻ đường cao AH của tam giác ABC. Chứng mình rằng tứ giác ADEH là hình thang vuông.
c) Gọi I là giao điểm của AH với BD, đường thẳng EI cắt AB tại F. Chứng minh rằng tứ giác ACEF là hình thang vuông.
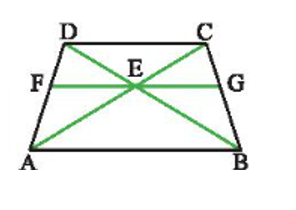
Câu 4: Cho hình thang ABCD có AB // CD. Qua giao điểm E của AC và BD, ta vẽ đường thẳng song song với AB cắt AD, BC lần lượt tại F và G (Hình 16). Chứng minh rằng EG là tia phân giác góc CEB.
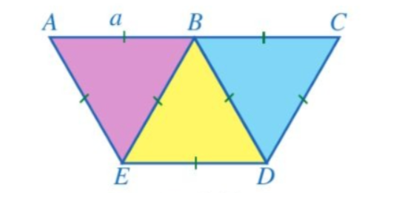
Câu 5. Người ta ghép ba hình tam giác đều có độ dài cạnh là a với vị trí như hình vẽ.
a) Chứng minh ba điểm A, B, C thẳng hàng.
b) Chứng minh tứ giác ACDE là hình thang cân.
c) Tính diện tích của tứ giác ACDE theo a.
Câu 1.
a) Ta có: $MN\perp AH$ (gt)
Và $BC\perp AH$ (AH là đường cao của tam giác ABC) ⇒MN//BC
Suy ra BCMN là hình thang
b) $\widehat{NBM}=\widehat{MBC}$ (BM là tia phân giác góc B)
Suy ra $\widehat{BMN}=\widehat{NBM}\Rightarrow \Delta BMN$ cân tại N.
Vậy BN=MN
Câu 3:
a) Xét ΔABD và ΔEBD ta có:
AB = BE (gt)
BD là cạnh chung
$\widehat{ABD}=\widehat{DBE}$ (BD là tia phân giác của góc B)
Do đó ΔABD = ΔEBD(c.g.c)
b) Ta có: $\widehat{DBE}=\widehat{BAD}$ (ΔEBD = ΔABD)
Mà $\widehat{BAD}=90^{\circ}$ (ΔABD vuông tại A)
Nên $\widehat{DEB}=90^{\circ}\Rightarrow DE\perp BC$
Mặt khác $AH\perp BC$ (gt) do đó DE // AH
⇒ Tứ giác ADEH là hình thang
Lại có $\widehat{AHE}=90^{\circ}(AH\perp BC)$
Vậy tứ giác ADEH là hình thang vuông.
c) Ta có BE = BA(gt) ⇒Tam giác cân tại B.
Mà BD là tia phân giác của góc B. Do đó BD là đường cao của tam giác BAE.
Xét ΔBAE có: AH, BD là hai đường cao cắt nhau tại I
⇒ I là trực tâm của tam giác BAE.
⇒ EF là đường cao của tam giác BAE
⇒ EF $\perp$ AB
Mà AC⊥AB ⇒ EF//AC
Vậy tứ giác ACEF là hình thang.
Mà $\widehat{CAF}=90^{\circ}$. Do đó tứ giác ACEF là hình thang vuông.
Câu 4:
Xét tam giác ACD và BDC ta có:
AD = BC (gt)
AC = BD (gt)
CD chung
Suy ra $\Delta ACD=\Delta BDC$ (c.c.c)
⇒ $\widehat{ACD}=\widehat{BDC}$
Ta có: FG // CD suy ra $\widehat{BEG}=\widehat{BDC}$ (đồng vị),
$\widehat{GEC}=\widehat{ADC}$ (so le trong)
Suy ra $\widehat{BEG}=\widehat{GEC}$ hay EG là tia phân giác góc CEB.
Câu 5.
a) Vì 3 tam giác ABE, BED, BDC là các tam giác đều có cạnh bằng nhau nên:
$\widehat{ABE}=\widehat{DBE}\Rightarrow $ AB//ED
$\widehat{CBD}=\widehat{EBD}\Rightarrow $ BC//ED
Như vậy AB và BC cùng // với ED lại có chung điểm B nên 3 điểm A, B, C thẳng hàng. (đpcm)
b) Xét tứ giác ACDE có: AC // DE
=> tứ giác ACDE là hình thang
2 cạnh bên AE = CD (đều = a)
=> ACDE là hình thang cân.
c) Diện tích của tứ giác ACDE = Tổng diện tích của 3 tam giác ABE, BED, BDC mà 3 tam giác ABE, BED, BDC đều bằng nhau nên ta chỉ cần tính diện tích của một tam giác BED.
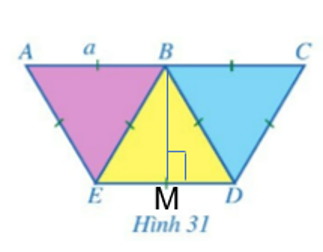
Gọi BM là đường cao của tam giác BED.
Khi đó $BM=\sqrt{a^{2}-(\frac{a}{2})^{2}}=\frac{a\sqrt{3}}{2}$
Diện tích tam giác BED là: $\frac{1}{2}.BM.ED=\frac{1}{2}.\frac{a\sqrt{3}}{2}.a=\frac{a^{2}\sqrt{3}}{4}$
Diện tích của tứ giác ACDE$=3.\frac{a^{2}\sqrt{3}}{4}=\frac{a^{2}\sqrt{3}.3}{4}$

Bình luận