Bài tập file word mức độ nhận biết bài 11: Hình thang cân
1. NHẬN BIẾT (7 câu)
Câu 1: Tìm các góc chưa biết của hình thang MNPQ có hai đáy là MN và QP trong mỗi trường hợp sau và nêu nhận xét của em
a) $\widehat{Q}=90^{\circ}$ và $\widehat{N}=125^{\circ}$
b) $\widehat{P}=\widehat{Q}=110^{\circ}$
Câu 2: Tìm các đoạn thẳng bằng nhau trong hình thang cân MNPQ có hai đáy là MN và PQ
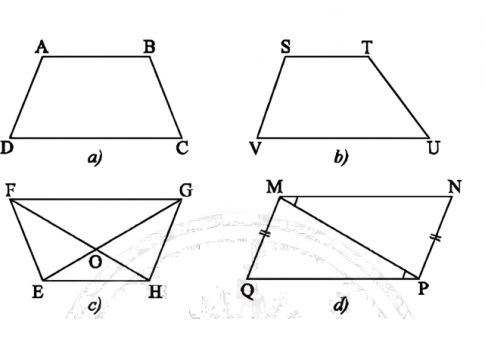
Câu 3: Sử dụng thước đo góc và thước đo độ dài để tìm hình thang cân trong các tứ giác ở hình vẽ.
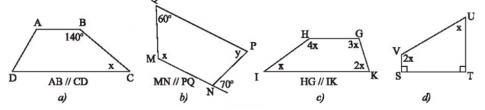
Câu 4: Tìm x và y ở các hình sau.
Câu 5. Cho tứ giác ABCD có AB = CD, BD là tia phân giác góc B. Chứng minh rằng ABCD là hình thang.
Câu 6. Cho hình thang cân ABCD có AB//CD. Chứng mình
Câu 7. Tứ giác nào trong hình vẽ là hình thang cân?
Câu 1:
a) Hình thang MNPQ (MN//PQ) có: $\widehat{Q}=90^{\circ}$
MNPQ là hình thang vuông.
Suy ra $\widehat{Q}=\widehat{M}=90^{\circ}$ và $\widehat{P}=180^{\circ}-\widehat{N}=180^{\circ}-125^{\circ}=55^{\circ}$
b) Hình thang MNPQ (MN//PQ) có: $\widehat{P}=\widehat{Q}=110^{\circ}$
MNPQ là hình thang cân
Suy ra $\widehat{M}=\widehat{N}=180^{\circ}-110^{\circ}=70^{\circ}$
Câu 2:
MQ = NP
MP = NQ
Câu 3:
a) c) là hình thang cân
Câu 4:
a) $x=180^{\circ}-140^{\circ}=40^{\circ}$
b) $x=180^{\circ}-60^{\circ}=120^{\circ}$
MN // PQ suy ra y = $\widehat{N}$ngoài = $70^{\circ}$ (so le trong)
c) Ta có: 4x + 3x + 2x + x = 360osuy ra 10x=360ohay x = 36∘
d) Ta có: x+2x=180osuy ra 3x = 180ohay x = 60o
Câu 5.
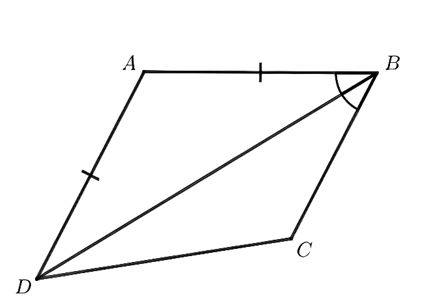
Xét tam giác ABD có AB=AD (gt)
⇒ΔABD cân tại A ⇒ $\widehat{ABD}=\widehat{ADB}$
Mà $\widehat{ADB}=\widehat{DBC}$ (BD là tia phân giác của góc B)
Do đó $\widehat{ADB}=\widehat{DBC}$
Mà $\widehat{ADB}$ và $\widehat{DBC}$ so le trong
⇒AD // BC
Vậy ABCD là hình thang.
Câu 6.
ABCD là hình thang cân nên: $\widehat{DAB}=\widehat{CBA}$ ; AD=BC.
Xét tam giác ADB và tam giác BCA, ta có:
AD=BC
$\widehat{DAB}=\widehat{CBA}$
AB chung
=> tam giác ADB = tam giác BCA (c.g.c)
=> $\widehat{DAB}=\widehat{CBA}$ (2 góc tương ứng)
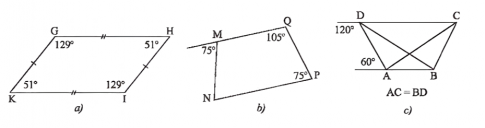
Câu 7.
a) Ta có: $\widehat{G}+\widehat{K}=129^{\circ}+51^{\circ}=180^{\circ}$
Mà $\widehat{G}$ và $\widehat{K} là hai góc trong cùng phía suy ra GH // KI
⇒ GHKI là hình thang
$\widehat{G}\neq \widehat{H}$
$\widehat{K}\neq \widehat{I}$
Suy ra GHIK không là hình thang cân
b) Ta có: $\widehat{NMQ}+\widehat{M}$ ngoài =180∘(hai góc kề bù)
Do đó $\widehat{NMQ}+75^{\circ}=180^{\circ}$
⇒ $\widehat{NMQ}=180^{\circ}-75^{\circ}=105^{\circ}$
Ta có $\widehat{Q}+\widehat{P}=105^{\circ}+75^{\circ}=180^{\circ}$
Mà $\widehat{Q}$ và $\widehat{P}$ là hai góc trong cùng phía suy ra MQ // PN
⇒ MQPN là hình thang
Lại có: $\widehat{Q}=\widehat{QMN}=105^{\circ}$
Do đó MQPN là hình thang cân.

Bình luận