Lý thuyết trọng tâm Toán 8 kết nối bài 14: Hình thoi và hình vuông
Tổng hợp kiến thức trọng tâm Toán 8 kết nối tri thức bài 14: Hình thoi và hình vuông. Tài liệu nhằm củng cố, ôn tập lại nội dung kiến thức bài học cho học sinh dễ nhớ, dễ ôn luyện. Kéo xuống để tham khảo
CHƯƠNG 3. TỨ GIÁC
BÀI 14: HÌNH THOI VÀ HÌNH VUÔNG
1. HÌNH THOI
Khái niệm hình thoi và tính chất của nó
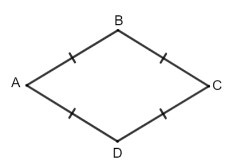
Kết luận:
Hình thoi là tứ giác có bốn cạnh bằng nhau.
Câu hỏi:
- Hình thoi là hình bình hành vì có hai cạnh đối bằng nhau.
- Tính chất của hình thoi:
+ Hình thoi có các cặp cạnh đối song song và bằng nhau.
+ Hình thoi có các góc đối bằng nhau.
+ Hình thoi có hai đường chéo cắt nhau tạo trung điểm của mỗi đường.
Hoạt động 1:
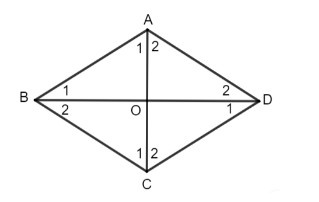
- a) Ta có AB = AD nên ABD là tam giác cân tại A
- b) Ta có O là trung điểm của BD (do ABCD là hình thoi nên cũng là hình bình hành)
⇒ OB = OD
Xet tam giác AOB và AOD ta có:
AO chung
OB = OD
AB = AD
⇒ ΔAOB = ΔAOD (c.c.c) ⇒ A1=A2
Suy ra AC là phân giác A
Mà tam giác ABD cân suy ra AC vuông góc với BD
Định lí 1:
Trong hình thoi:
- a) Hai đường chéo vuông góc với nhau;
- b) Hai đường chéo là các đường phân giác của các góc trong hình thoi.
Ví dụ 1:
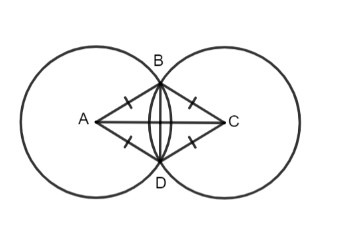
- a) Vì hai đường tròn tâm A và C có cùng bán kính, cắt nhau tại B, D nên AB = AD = CD = CB. Vậy theo định nghĩa, tứ giác ABCD là hình thoi.
- b) Từ câu a và theo Định lí 1 ta có AC
Dấu hiệu nhận biết hình thoi
Định lí 2:
- a) Hình bình hành có hai cạnh kề bằng nhau là hình thoi.
- b) Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
- c) Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.
Câu hỏi:
GT | ABCD là hình bình hành, BD là đường phân giác của D, B |
KL | ABCD là hình thoi |
Ví dụ 2:
- a) Tứ giác ABCD là hình bình hành vì có các góc đối bằng nhau: A=C, B=D.
Mặt khác, ta lại có hai cạnh kề AB và BC bằng nhau.
Do đó, tứ giác ABCD là hình thoi.
- b) Tứ giác MNPQ không phải là hình thoi vì hai cạnh kề MN và NP không bằng nhau.
Luyện tập 1:
Hình a) là hình thoi
Vì là hình bình hành (có hai đường chéo cắt nhau ở trung điểm của mỗi đường) có hai đường chéo vuông góc với nhau.
Hình b) là hình thoi
Vì là hình bình hành (có một cặp cạnh đối song song và bằng nhau) có một đường chéo là đường phân giác của một góc.
Hình c) không là hình thoi vì bốn cạnh không bằng nhau.
2. HÌNH VUÔNG
Khái niệm hình vuông và tính chất của nó
Kết luận:
Hình vuông là tứ giác có bốn góc vuông và bốn cạnh bằng nhau.
Hoạt động 2:
+ Vì hình vuông có bốn góc vuông nên hình vuông cũng là hình chữ nhật nên có hai đường chéo bằng nhau.
+ Vì hình vuông có bốn cạnh bằng nhau nên hình vuông cũng là hình thoi nên có hai đường chéo vuông góc với nhau.
Định lí 3:
Trong một hình vuông, hai đường chéo bằng nhau, vuông góc với nhau, cắt nhau tại trung điểm mỗi đường và là các đường phân giác của các góc của hình vuông.
Dấu hiệu nhận biết hình vuông
Định lí 4:
- a) Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
- b) Hình chữ nhật có hai đường chéo vuông góc là hình vuông.
- c) Hình chữ nhật có một đường chéo là đường phân giác của một góc là hình vuông.
Chú ý:
+ Hình thoi có một góc vuông là hình vuông.
+ Hình thoi có hai đường chéo bằng nhau là hình vuông.
Câu hỏi:
GT | ABCD là hình chữ nhật, AB = AC |
KL | ABCD là hình vuông |
Ví dụ 3 (SGK – tr.70)
Luyện tập 2:
- a) Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông
- b) Hình chữ nhật có một đường chéo là đường phân giác của một góc là hình vuông
- c) Hình chữ nhật có hai đường chéo vuông góc là hình vuông.
Vận dụng:
- a) Tứ giác nhận được có các cạnh bằng nhau và bằng đoạn thẳng AB nên nó là hình thoi
- b) Nếu OA = OB thì hai đường chéo của hình thoi bằng nhau nên theo Chú ý, nó là hình vuông.
Bình luận