BÀI 14. HÌNH THOI VÀ HÌNH VUÔNG

I. HÌNH THOI

HĐ1. Cho hình thoi ABCD có hai đường chéo AC, BD cắt nhau tại O (H.3.48)

1. có cân tại A không?
2. 

Đáp án chuẩn:

a) ABD cân tại A

b) Chứng minh (c.c.c) ⇒ =>  AC là phân giác

Mà tam giác ABD cân => AC vuông góc với BD

LT 1. Trong Hình 3.51, hình nào là hình thoi? Vì sao?

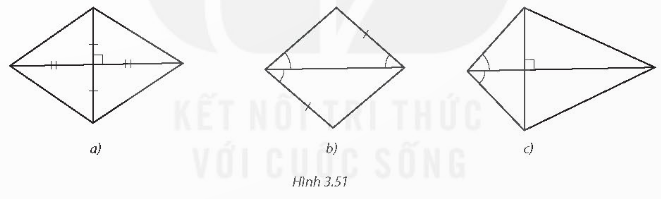
Đáp án chuẩn:

Hình a là hình thoi vì là hình bình hành có hai đường chéo vuông góc với nhau.

Hình b là hình thoi vì là hình bình hành có một đường chéo là đường phân giác của một góc.

II. HÌNH VUÔNG

HĐ2. Hãy giải thích tại sao hai đường chéo của hình vuông bằng nhau và vuông góc với nhau.

Đáp án chuẩn:

+) Hình vuông cũng là hình chữ nhật nên có hai đường chéo bằng nhau

+) Hình vuông cũng là hình thoi nên có hai đường chéo vuông góc với nhau

LT 2. Với mỗi hình dưới đây, ta dùng dấu hiệu nhận biết nào để khẳng định đó là hình vuông?

Đáp án chuẩn:

a) Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông

b) Hình chữ nhật có một đường chéo là đường phân giác của một góc là hình vuông

c) Hình chữ nhật có hai đường chéo vuông góc

III. GIẢI BÀI TẬP CUỐI SGK

Bài 3.29. Tìm các hình thoi và hình vuông trong Hình 3.55

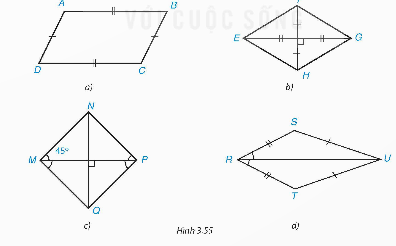
Đáp án chuẩn:

a) Tứ giác ABCD là hình bình hành 

b) Tứ giác EFGH là hình thoi 

c) Tứ giác MNPQ là hình vuông 

d) Tứ giác RSUT là hình cái diều 

Bài 3.30. Cho tam giác ABC, D là một điểm nằm giữa B và C. Qua D kẻ các đường thẳng song song với AB, AC, chúng cắt các cạnh AC, AB lần lượt tại E, F

1. Tứ giác AEDF là hình gì? Vì sao?
2. Nếu tam giác ABC cân tại A thì điểm D ở vị trí nào trên canh BC để tứ giác AEDF là hình thoi?
3. Nếu tam giác ABC vuông tại A thì tứ giác AEDF là hình gì?
4. Nếu tam giác ABC vuông cân tại A thì điểm D ở vị trí nào trên cạnh BC để AEDF là hình vuông? 

Đáp án chuẩn:

a) Tứ giác AEDF là hình bình hành. Vì có DE // AF, DF // AE 

b) D là trung điểm của BC

c) AEDF là hình chữ nhật

d) D là trung điểm cạnh BC 

Bài 3.31. Chứng minh rằng các trung điểm của bốn cạnh trong một hình chữ nhật là các đỉnh của một hình thoi.

Đáp án chuẩn:

Chứng minh EF = FG = GH = HE

Tứ giác EFGH là hình thoi.

Bài 3.32. Chứng minh rằng các trung điểm của bốn cạnh trong một hình thôi là các đỉnh của một hình chữ nhật.

Đáp án chuẩn:

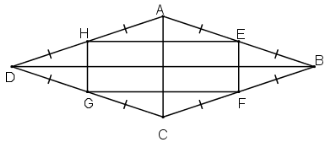
Chứng minh HEFG là hình bình hành (1)

Gọi AC và BD cắt nhau tại O OAD = OAB = OCD = OCB

OH = OE = OF = OG (2)

Từ (1) và (2)  => HEFG là hình chữ nhật.

Bài 3.33. Cho hình chữ nhật ABCD có chu vi bằng 36 cm. Gọi M là trung điểm của cạnh BC. Biết MA MD. Tính độ dài các cạnh của hình chữ nhật ABCD (H.3.56)

Đáp án chuẩn:

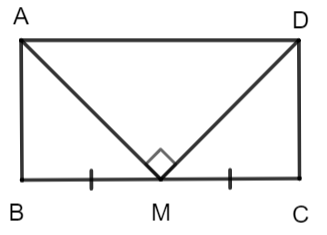
AB = CD = 6 (cm); BC = AD = 12 (cm).