Giải câu 30 bài 4: Diện tích hình thang sk Toán hình 8 tập 1 Trang 126
Câu 30 : Trang 126 sgk toán 8 tập 1
Trên hình 143 ta có hình thang ABCD với đường trung bình EF và hình chữ nhật GHIK. Hãy so sánh diện tích hai hình này, từ đó suy ra một cách chứng minh khác về công thức diện tích hình thang.
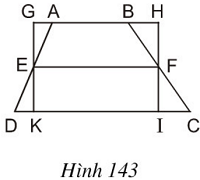
Xét ∆AEG và ∆DEK có:
AE = DE (do E là trung điểm của AD)
$\widehat{AEG} = \widehat{DEK}$
$\widehat{EKD} = \widehat{KGA} = 90^{0}$
=>∆AEG = ∆DEK (cạnh huyền - góc nhọn)
Tương tự ta có: ∆BFH = ∆CFI
=> SABCD = SAEKIFB + SDEK + SCFI = SAEKIFB + SAEG + SBFH = SGHIK
=>SABCD = SGHIK = EF. GK mà \(EF = {{AB + CD} \over 2}\)
=> SABCD = \({S_{ABC{\rm{D}}}} = {{AB + C{\rm{D}}} \over 2}.GK\)
Vậy diện tích hình thang bằng tích của đường trung bình hình thang với chiều cao.
Từ khóa tìm kiếm Google: giải câu 30 trang 126 sgk Toán 8 tập 1, giải bài tập 30 trang 126 Toán 8 tập 1, câu 30 trang 126, Câu 30 bài 4: Diện tích hình thang - sgk Toan 8 tập 1
Giải những bài tập khác
Giải bài tập những môn khác
Giải sgk lớp 8 cánh diều
Giải SBT lớp 8 kết nối tri thức
Giải SBT lớp 8 chân trời sáng tạo
Soạn SBT lớp 8 cánh diều
Trắc nghiệm 8 Kết nối tri thức
Trắc nghiệm 8 Chân trời sáng tạo
Trắc nghiệm 8 Cánh diều
Bộ đề thi, đề kiểm tra lớp 8 chân trời sáng tạo
Giáo án lớp 8
Bình luận