Đề số 6: Đề kiểm tra toán 8 Kết nối bài 13 Hình chữ nhật
ĐỀ 6
I. Phần trắc nghiệm (4 điểm)
(Chọn chữ cái trước câu trả lời đúng nhất.)
Câu 1: Hãy chọn câu sai.
- A. Hình thang cân có một góc vuông là hình chữ nhật
- B. Hình bình hành có một góc vuông là hình chữ nhật
- C. Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật
- D. Hình thang có một góc vuông là hình chữ nhật
Câu 2: Hãy chọn câu trả lời đúng. Hình bình hành ABCD là hình chữ nhật khi:
- A. AB = BC
- B. AC ⊥ BD
- C. AC = BD
- D. BC = CD
Câu 3: Khoanh tròn vào phương án sai
- A. Trong tam giác vuông đường trung tuyến ứng với cạnh huyền và bằng nửa cạnh huyền.
- B. Trong tam giác, đường trung tuyến với với một cạnh và bằng nửa cạnh ấy thì tam giác đó là tam giác vuông.
- C. Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền thì vuông góc với cạnh huyền.
- D. Trong tam giác vuông, đường trung tuyến ứng với cạnh góc vuông không bằng cạnh ấy.
Câu 4: P là một điểm bên trong hình chữ nhật ABCD sao cho PA = 3cm, PD = 4cm và PC = 5cm.Vậy PB, tính bằng cm, bằng:
- A. $3\sqrt{2}$
- B. $2\sqrt{2}$
- C. $4\sqrt{2}$
- D. $2\sqrt{3}$
II. Phần tự luận (6 điểm)
Câu 1 (6 điểm): Cho tam giác ABC vuông tại A (AB < AC). Gọi D là trung điểm của BC. Vẽ DE // AB, vẽ DF // AC (E ∈ AC, F ∈ AB).
a) Chứng minh rằng tứ giác AEDF là hình chữ nhât.
b) Chứng minh rằng tứ giác BFED là hình bình hành.
Trắc nghiệm: (Mỗi câu đúng tương ứng với 1 điểm)
Câu hỏi | Câu 1 | Câu 2 | Câu 3 | Câu 4 |
Đáp án | D | C | C | A |
Tự luận:
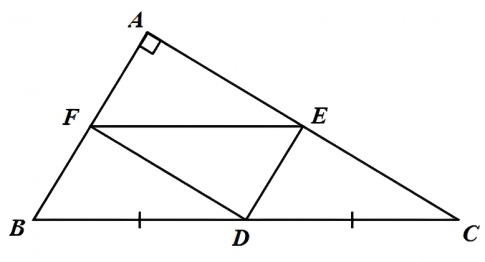
a) Tứ giác AEDF có:
AE // DF (AC // FD, E ∈AC)
AF // DE (AB // DE, F ∈ AB)
=> AEDF là hình bình hành.
Mà $\widehat{FAE}=90^{\circ}$ (ΔABC vuông tại A)
Nên AEDF là hình chữ nhât.
b) ΔABC có D là trung điểm của BC và FD // AC
=> F là trung điểm của AB.
ΔABC có D là trung điểm của BC và DE // AB
=> E là trung điểm của AC
=> EF là đường trung bình của tam giác ABC
=> EF // BC và $EF = \frac{1}{2} BC $
Lại có $BD = \frac{1}{2} BC$ (Vì D là trung điểm của BC)
⇒ EF // BD và EF = BD
Vậy tứ giác BFED là hình bình hành (dấu hiệu nhận biết).
Xem toàn bộ: Đề kiểm tra Toán 8 KNTT bài 13: Hình chữ nhật

Bình luận