Lý thuyết trọng tâm toán 7 kết nối bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác
Tổng hợp kiến thức trọng tâm toán 7 kết nối tri thức bài 14 Trường hợp bằng nhau thứ hai và thứ ba của tam giác. Tài liệu nhằm củng cố, ôn tập lại nội dung kiến thức bài học cho học sinh dễ nhớ, dễ ôn luyện. Kéo xuống để tham khảo
BÀI 14. TRƯỜNG HỢP BẰNG NHAU THỨ HAI VÀ THỨ BA CỦA TAM GIÁC
1. TRƯỜNG HỢP BẰNG NHAU THỨ HAI CỦA TAM GIÁC: CẠNH – GÓC – CẠNH (C.G.C)
HĐ1:
HĐ2:
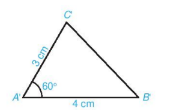
- Các cạnh tương ứng của hai tam giác ABC và A’B’C’ bằng nhau.
- Hai tam giác ABC và A’ B’ C’ bằng nhau theo trường hợp cạnh – cạnh – cạnh.
- Các tam giác vẽ được đều bằng nhau.
Chú ý:
Trong tam giác ABC, góc BAC được gọi là góc xen giữa hai cạnh AB và AC của tam giác ABC.
Định lí:
Trường hợp bằng nhau cạnh – góc – cạnh (c.g.c)
Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
GT | ΔABCvà ΔA'B'C' AB = A’B’, AC = A’C’, $\widehat{A}$=$\widehat{A'}$ |
KL | ΔABC=ΔA'B'C' |
Câu hỏi:
+ Xét hai tam giác ABC và MNP có:
AB = MN
$\widehat{BAC}$=$\widehat{NMP}$
AC = MP
⇒ΔABC=ΔMNP
Hoặc ΔBAC=ΔNMP.
Ví dụ 1 (SGK – tr71)
Luyện tập 1:
+) Xét tam giác MNP có:
$\widehat{M}$=180$^{\circ}$-50$^{\circ}$-70$^{\circ}$=60$^{\circ}$.
+ Xét hai tam giác ABC và MNP có:
AB = MN
AC = MP
$\widehat{A}$=$\widehat{P}$
⇒ΔABC=ΔMNP (c.g.c)
Vận dụng:
a) AC = AB + BC = DC + BC = DB
b) Xét hai tam giác OAC và ODB có:
AO = DO
$\widehat{A}$=$\widehat{D}$
AC = DB (chứng minh trên)
⇒ΔOAC=ΔODB (c.g.c)
2. TRƯỜNG HỢP BẰNG NHAU THỨ BA CỦA TAM GIÁC: GÓC – CẠNH – GÓC (G.C.G)
HĐ3:
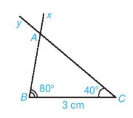
HĐ4:
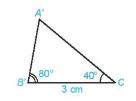
- Các cạnh tương ứng của hai tam giác ABC và A’B’C’ bằng nhau.
- Hai tam giác ABC và A’B’ C’ bằng nhau theo trường hợp cạnh – cạnh – cạnh.
- Các tam giác HS vừa vẽ đều bằng nhau.
Chú ý:
Trong tam giác ABC, hai góc $\widehat{ABC}$,$\widehat{ACB}$ được gọi là các góc kề cạnh BC của tam giác ABC.
Định lí:
Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.
GT | ΔABCvà ΔA'B'C' AB = A’B’ $\widehat{A}$=$\widehat{A'}$, $\widehat{B}$=$\widehat{B'}$ |
KL | ΔABC=ΔA'B'C' |
Câu hỏi:
+ Xét hai tam giác ABC và MNP có:
$\widehat{ABC}$=$\widehat{MNP}$
BC = PN
$\widehat{ACB}$=$\widehat{MPN}$
⇒ΔABC=ΔMNP
Ví dụ 2 (SGK – tr72)
Luyện tập 2:
Xét tam giác ABD và CBD có:
$\widehat{ABD}$=$\widehat{CBD}$
$\widehat{ADB}$=$\widehat{CDB}$
ΔABD=ΔCBD (g.c.g)
Thử thách nhỏ:
$\widehat{C}$=180$^{\circ}$-$\widehat{A}$-$\widehat{B}$
=180$^{\circ}$-$\widehat{A'}$-$\widehat{B'}$=$\widehat{C'}$.
Xét tam giác ABC và A’B’C’ có:
$\widehat{A}$=$\widehat{A'}$
AC = A’C’
$\widehat{C}$=$\widehat{C'}$
ΔABD=ΔA'B'C' (g.c.g)
Bạn Lan nói đúng.
Bình luận