Giải câu 1 trang 141 sách toán VNEN lớp 7 tập 1

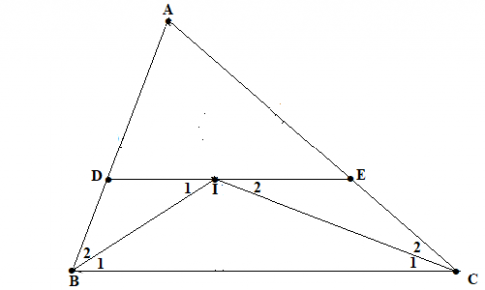
DE // BC (giả thiết) $\Rightarrow $ $\widehat{B_{1}} = \widehat{I_{1}}$ và $\widehat{C_{1}} = \widehat{I_{2}}$ (các góc ở vị trí so le trong). (1)

Mà BI, CI là tia phân giác của góc B và góc C $\Rightarrow $ $\widehat{B_{1}} = \widehat{B_{2}}$ và $\widehat{C_{1}} = \widehat{C_{2}}$. (2)

Từ (1) và (2): $\widehat{B_{2}} = \widehat{I_{1}}$ và $\widehat{C_{2}} = \widehat{I_{2}}$.

Suy ra các tam giác DBI và ECI là các tam giác cân tại D và E.

$\Rightarrow $ DB = DI và EC = EI

Lại có: DE = DI + IE nên DE = DB + CE.