A. Hoạt động khởi động

Thực hiện các hoạt động sau (sgk trang 129

B. Hoạt động hình thành kiến thức

1. a) Đọc kĩ nội dung sau (sgk trang 130)

b) Em hãy vẽ tam giác ABC cân tại A theo hướng dẫn sau (sgk trang 130)

c) Điền cụm từ thích hợp vào chỗ trống (…)

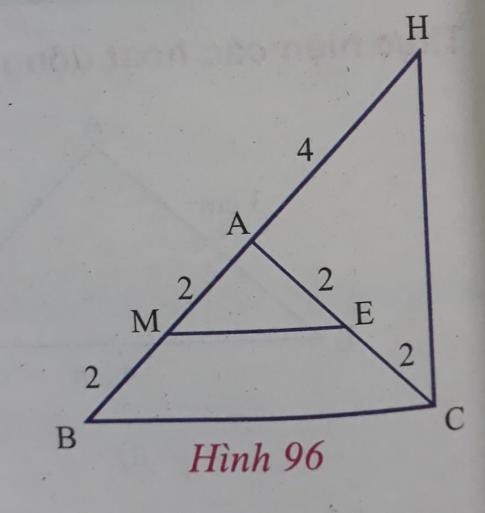
Cho hình 96. Tìm các tam giác cân trong hình đó.

Trả lời:

c) Nhìn hình 96, ta xác định được các tam giác cân sau:

2. a) – Em hãy đo các góc B và C ở hình 97 và so sánh hai góc đó.

- Kẻ AD là tia phân giác của $\widehat{BAC}$. Em hãy chứng tỏ $\widehat{ABC} = \widehat{ACB}$ bằng những kiến thức đã học và viết vào vở.

b) Đọc kĩ nội dung sau (sgk trang 131)

c) Em hãy chứng minh Định lí 2 (nêu ở dòng thứ hai trong khung màu ở trên (h.98b)) và ghi vào vở.

c) Điền vào chỗ trống (…)

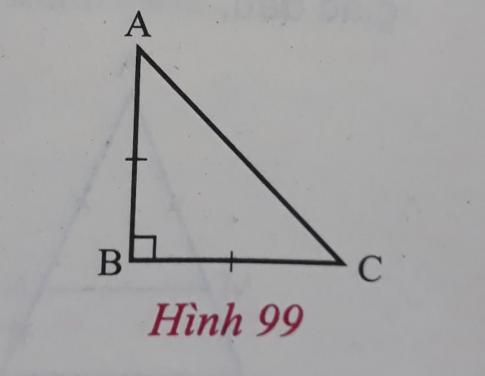
Ở hình 99 có:

$\bigtriangleup ABC$ cân tại A (giả thiết) $\Rightarrow $ $\widehat{B} = \widehat{C}$,

$\bigtriangleup ABC$ vuông tại A (giả thiết).

Suy ra $\widehat{B} + \widehat{C} = 90^{\circ} \Rightarrow \widehat{B} = \widehat{C} = … $.

Ghi nhớ: Trong tam giác vuông cân, mỗi góc nhọn có số đo bằng $45^{\circ}$.

Trả lời:

a) - $\widehat{B} = \widehat{C}$

- Chứng minh: $\widehat{ABC} = \widehat{ACB}$

Xét $\bigtriangleup ADB$ và $\bigtriangleup ADC$ có:

AD chung;

$\widehat{BAD} = \widehat{CAD}$ (giả thiết);

AB = AC (giả thiết);

$\Rightarrow $ $\bigtriangleup ADB = \bigtriangleup ADC$ (c.g.c).

$\Rightarrow $ $\widehat{ABC} = \widehat{ACB}$ (hai góc tương ứng).

c) Kẻ đường cao từ đỉnh A cắt BC tại D:

Xét $\bigtriangleup ADB$ và $\bigtriangleup ADC$ có:

AD chung;

$\widehat{BDA} = \widehat{CDA} = 90^{\circ}$ (theo cách vẽ);

$\widehat{BAD} = \widehat{CAD}$ (cùng phụ với hai góc có số đo bằng nhau).

$\Rightarrow $ $\bigtriangleup ADB = \bigtriangleup ADC$ (g.c.g).

$\Rightarrow $ AB = AC hay tam giác ABC cân tại A.

d) Ở hình 99 có:

$\bigtriangleup ABC$ cân tại A (giả thiết) $\Rightarrow $ $\widehat{B} = \widehat{C}$,

$\bigtriangleup ABC$ vuông tại A (giả thiết).

Suy ra $\widehat{B} + \widehat{C} = 90^{\circ} \Rightarrow \widehat{B} = \widehat{C} = 45^{\circ}$.

3. a) – Vẽ $\bigtriangleup ABC$ có AB = BC = CA vào vở.

- Đo và so sánh các góc của tam giác ABC (h.100)

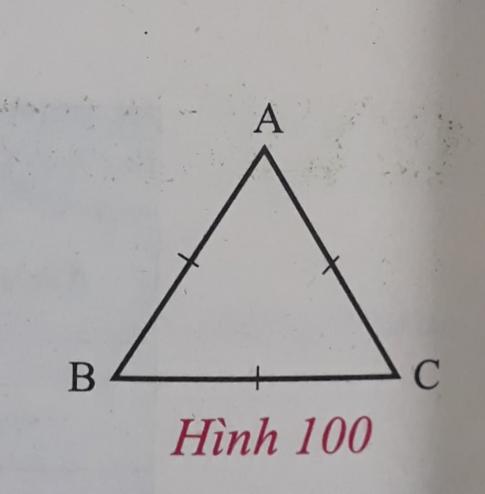
- Không cần dùng thước để đo, em có thể cho biết số đo các góc của tam giác ABC không?

b) Đọc kĩ nội dung sau (sgk trang 132)

c) Em hãy đọc kĩ cách chứng minh tính chất 1 như dưới đây, sau đó tự chứng minh tính  chất 3 vào vở:

Chứng minh tính chất 1 (sgk trang 132).

d) Chứng minh tính chất: Nếu một tam giác cân có một góc bằng $90^{\circ}$ thì tam giác đó là tam giác đều.

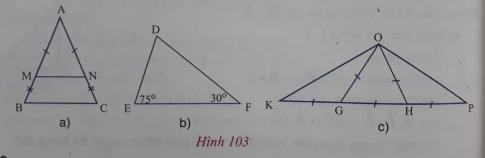
e) Quan sát các hình vẽ ở hình 103. Tìm trong các hình đó các tam giác cân, tam giác đều,

Trả lời:

a) – Các em vẽ lại hình 100 vào vở

- Số đo các góc của tam giác ABC là: $\widehat{A} = \widehat{B} = \widehat{C} = 60^{\circ}$.

- Không dùng thước, ta vẫn có thể xác định số đo các góc của tam giác ABC như sau
+ Xét $\bigtriangleup ABC$ có: AB = AC nên là tam giác cân tại A, suy ra: $\widehat{B} = \widehat{C}$. (1)

+ Xét $\bigtriangleup ABC$ có: CB = CA nên là tam giác cân tại C, suy ra: $\widehat{A} = \widehat{B}$. (2)

Mà: $\widehat{A} + \widehat{B} + \widehat{C} = 180^{\circ}$

+ Từ (1) và (2): $\widehat{A} = \widehat{B} = \widehat{C} = 180 : 3 = 60^{\circ}$.

c) Do $\bigtriangleup ABC$ có $\widehat{A} = \widehat{B} = \widehat{C}$ nên $\bigtriangleup ABC$ vừa cân tại A vừa cân tại C.

$\Rightarrow $ AB = AC và AC = BC hay AB = BC = CA, suy ra $\bigtriangleup ABC$ đều.

d) TH1: Giả sử $\bigtriangleup ABC$ cân tại A và có $\widehat{A} = 60^{\circ}$ ta cần chứng minh $\bigtriangleup ABC$ có AB = AC = BC hoặc $\widehat{A} = \widehat{B} = \widehat{C} = 60^{\circ}$.

Chứng minh:

Xét $\bigtriangleup ABC$ cân tại A $\Rightarrow $ $\widehat{B} =\widehat{C}$ và $\widehat{A} = 60^{\circ}$.

Mà: $\widehat{A} + \widehat{B} + \widehat{C} = 180^{\circ}$

$\Rightarrow $ $\widehat{B} =\widehat{C} = (180^{\circ} – 60^{\circ}) : 2 = 60^{\circ}$

Hay $\bigtriangleup ABC$ có $\widehat{A} = \widehat{B} = \widehat{C} = 60^{\circ}$ nên là tam giác đều.

TH2: Giả sử $\bigtriangleup ABC$ cân tại A và có $\widehat{B} = 60^{\circ}$ ta cần chứng minh $\bigtriangleup ABC$ có AB = AC = BC hoặc $\widehat{A} = \widehat{B} = \widehat{C} = 60^{\circ}$.

Chứng minh:

Xét $\bigtriangleup ABC$ cân tại A $\Rightarrow $ $\widehat{B} =\widehat{C} = 60^{\circ}$.

Mà: $\widehat{A} + \widehat{B} + \widehat{C} = 180^{\circ}$

$\Rightarrow $ $\widehat{A} = 180^{\circ} – 2\times 60^{\circ} = 60^{\circ}$.

Hay $\bigtriangleup ABC$ là tam giác đều (đpcm).

e) Ở hình 103a)

+ $\bigtriangleup ABC$ là tam giác cân tại A vì có AB = AC (tổng hai đoạn thẳng tương ứng bằng nhau).

+ $\bigtriangleup AMN$ là tam giác cân tại A vì có AM = AN.

Ở hình 103b) $\bigtriangleup DEF$ không phải là tam giác cân, cũng không phải là tam giác đều.

Ở hình 103c)

+ $\bigtriangleup GKO$ là tam giác cân tại G vì có KG = GO.

+ $\bigtriangleup OHP$ là tam giác cân tại H vì có OH = HP.

+ $\bigtriangleup OGH$ là tam giác đều vì có OG = GH = HO.