A. B. Hoạt động khởi động và hình thành kiến thức

1. Thực hiện các hoạt động sau để biết tính chất về tổng ba góc trong tam giác

a) Đọc và làm theo

- Lấy một tờ giấy cắt thành hình tam giác. Sau đó cắt rời hai góc rồi ghép lại như hình 40. Nêu nhận xét.

- Vẽ một tam giác. Dùng thước đo góc, đo và cho biết số đo các góc của tam giác đó (h.41)

Cho biết tổng số đo của tam giác đó.

So sánh tổng số đo ba góc của tam giác với kết quả của bạn khác. Nêu nhận xét.

Trả lời

Hình 41: Tổng số đo các góc của tam giác là:

           85$^{0}$ + 55$^{0}$ + 40$^{0}$ = 180$^{0}$

b) Đọc và làm theo

- Vẽ một tam giác ABC.

- Qua điểm A vẽ một đường thẳng xy song song với BC (h.42)

- Khi đó, $\widehat{xAB}$ = $\widehat{ABC}$ (vì đó la hai góc so le trong) và $\widehat{CAy}$ = $\widehat{ACB}$ (vì đó la hai góc so le trong).

- Suy ra: $\widehat{B_{1}}$ + $\widehat{A_{3}}$ + $\widehat{C_{2}}$ = $\widehat{xAB}$ + $\widehat{BAC}$ + $\widehat{CAy}$ = 180$^{0}$

c) Đọc kĩ nội dung sau

• Định lí 1: Tổng ba góc của một tam giác bằng 180$^{0}$

d) Luyện tập

- Hãy nêu giả thiết và kết luận của định lí 1: Tổng ba góc của một tam giác bằng 180$^{0}$.

- Hãy chứng minh định lí đó.

Trả lời:

- Định lí 1:

+ Giả thiết của định lí 1 là: "tổng ba góc của một tam giác".

+ Kết luận của định lí 1 là: "bằng 180$^{0}$".

- Chứng minh định lí 1:

Cho tam giác ABC. Qua đỉnh A kẻ đường thẳng mn song song với BC.

Vì mn // Bc nên ta có: $\widehat{A_{2}}$ = $\widehat{B_{1}}$ và $\widehat{A_{3}}$ = $\widehat{C_{1}}$ (so le trong).

Lại có: $\widehat{A_{1}}$ + $\widehat{A_{2}}$ + $\widehat{A_{3}}$ = 180$^{0}$.

Mà  $\widehat{B_{1}}$ = $\widehat{A_{2}}$ và $\widehat{C_{1}}$ = $\widehat{A_{3}}$ nên suy ra $\widehat{A_{1}}$ + $\widehat{B_{1}}$ + $\widehat{C_{1}}$ = 180$^{0}$ (đpcm).

* Ghi nhớ:

• Tam giác có một góc vuông được gọi là tam giác vuông
• Trong một tam giác vuông, hai góc nhọn phụ nhau.

2. Thực hiện các hoạt động sau để hiểu thêm về góc ngoài của tam giác

a) Đọc và làm theo

- Vẽ tam giác ABC

Vẽ góc $\widehat{BCD}$ kề bù với góc $\widehat{BCA}$ (h.44).

* Ghi nhớ: Góc kề bù với một góc của tam giác gọi là góc ngoài của tam giác.

- Ở hình 44, $\widehat{BCD}$ là một góc ngoài của tam giác ABC.

- Hãy vẽ và đọc tên các góc ngoài của tam giác ABC.

Trả lời:

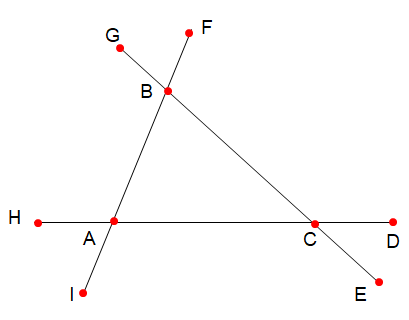
Các góc ngoài của tam giác ABC là: $\widehat{BCD}$; $\widehat{ACE}$; $\widehat{CAI}$; $\widehat{BAH}$; $\widehat{CBF}$; $\widehat{ABG}$

b) Đọc và làm theo

- Xét một góc ngoài $\widehat{BCD}$ của tam giác ABC (h.44).

- Đo và so sánh góc ngoài của tam giác với tổng hai góc trong không kề với nó là $\widehat{A}$ và $\widehat{B}$.

Trả lời:

Đo các góc và so sánh ta được:

$\widehat{A}$ + $\widehat{B}$ = $\widehat{BCD}$

- Chú ý: Do $\widehat{A}$ + $\widehat{B}$ + $\widehat{BCA}$ = 180$^{0}$ và $\widehat{BCA}$ + $\widehat{BCD}$ = 180$^{0}$, suy ra $\widehat{A}$ + $\widehat{B}$ = $\widehat{BCD}$

c) Đọc kĩ nội dung sau

• Định lí 2: Mỗi góc ngoài của một tam giác bằng tổng của hai góc trong không kề với nó.

d) Luyện tập

- Hãy nêu giả thiết và kết luận của định lí 2: Mỗi góc ngoài của một tam giác bằng tổng của hai góc trong không kề với nó.

- Hãy chứng minh định lí đó.

Trả lời:

- Định lí 2:

+ Giả thiết của định lí 2 là: "mỗi góc ngoài của một tam giác".

+ Kết luận của định lí 2 là: "bằng tổng của hai góc trong không kề với nó".

- Chứng minh định lí 2:

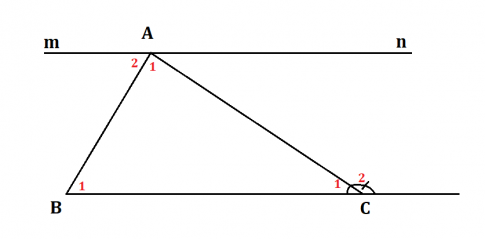
Cho tam giác ABC. Qua đỉnh A kẻ đường thẳng mn song song với BC.

Vì BC // mn nên ta có: $\widehat{A_{2}}$ = $\widehat{B_{1}}$ (so le trong). (1)

Lại có: $\widehat{mAC}$ = $\widehat{C_{2}}$ (so le trong) nên suy ra $\widehat{C_{2}}$ = $\widehat{A_{1}}$ + $\widehat{A_{2}}$. (2)

Từ (1) và (2) suy ra $\widehat{C_{2}}$ = $\widehat{A_{1}}$ + $\widehat{B_{1}}$ (đpcm).