A. Hoạt động khởi động

Viết các phân số sau dưới dạng số thập phân

Ta làm như sau: 

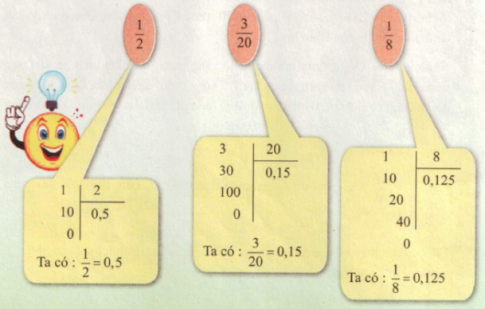
B. Hoạt động hình thành kiến thức

1. Đọc kĩ nội dung sau:

• Số thập phân hữu hạn

Các số thập phân 0,5; 0,15 và 0,125 còn gọi là số thập phân hữu hạn.

Ví dụ: Các số -2,5; 0,38; 7,125 là các số thập phân hữu hạn

2. a) Viết các số sau dưới dạng số thập phân: $\frac{5}{12}$; $\frac{4}{11}$.

Ta làm như sau:

b) Đọc kĩ nội dung sau

Số thập phân vô hạn tuần hoàn

• Số 0,4166.... là một số thập phân vô hạn tuần hoàn. Số 0,4166.... được viết gọn là 0,41(6), kí hiệu (6) chỉ rằng chữ số 6 được lặp lại vô hạn lần, số 6 gọi là chu kì của số thập phân vô hạn tuần hoàn 0,41(6).

Tương tự:

0,3636... = 0,(36) là một số thập phân vô hạn tuần hoàn có chu kì 36

-1,5454... = -1,(54) là số thập phân vô hạn tuần hoàn có chu kì 54.

c) Viết các phân số sau đây dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn và chỉ ra chu kì của nó: $\frac{7}{3}$; $\frac{-16}{5}$; $\frac{12}{25}$; $\frac{-19}{20}$; $\frac{7}{8}$.

Trả lời:

$\frac{7}{3}$ = 2,33333… = 2,(3) là một số thập phân vô hạn tuần hoàn có chu kì là 3;

$\frac{-16}{5}$ = -3,2 là một số thập phân hữu hạn;

$\frac{12}{25}$ = 0,48 là một số thập phân hữu hạn;

$\frac{-19}{20}$ = 0,95 là một số thập phân hữu hạn; 

$\frac{7}{8}$ = 0,875 là một số thập phân hữu hạn.

3. Đọc kĩ nội dung sau

• Người ta chứng minh được rằng mỗi số thập phân vô hạn tuần hoàn đều là một số hữu tỉ.
• Mỗi số hữu tỉ được biểu diễn bởi một số thập phân hữu hạn hoặ vô hạn tuần hoàn. Ngược lại, mỗi số thập phân hữu hạn hoặc vô hạn tuần hoàn đều biểu diễn một số hữu tỉ.

Ví dụ: 0,(2) = 0,(1).2 = $\frac{1}{9}$.2 = $\frac{2}{9}$