A. B. Hoạt động khởi động và hình thành kiến thức

1. Thực hiện các hoạt động sau để hiểu thêm về đường thẳng song song

a) Đọc và làm theo hướng dẫn

- Vẽ trên trang giấy một dường thẳng a và một điểm A không thuộc a. Vẽ một đường thẳng b //a mà b đi qua A (h.13)

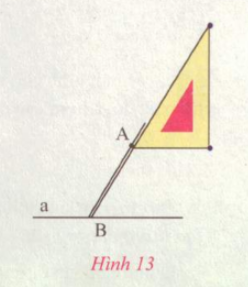
- Có thể vẽ bao nhiêu đường thẳng b như thế?

Trả lời:

Chỉ có thể vẽ được một đường thẳng b duy nhất.

b) Đọc kĩ nội dung sau

• Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó (Tiên đề Ơ - clit vè đường thẳng song song).

c) Luyện tập

Cho một điểm A không thuộc đường thẳng a. Câu nào sau đây là đúng?

(1) Nếu qua điểm A ta vẽ hai đường thẳng b và c cùng song song với a thì b $\equiv$ c.

(2) Nếu qua điểm A ta vẽ đường thẳng b song song với a thì không thể vẽ được đường thẳng c khác b mà c // a và c cũng qua A.

(3) Nếu qua điểm A ta vẽ đường thẳng b song song với a thì b là duy nhất.

(4) Qua điểm A ta vẽ được một và chỉ một đường thẳng b song song với a. 

Trả lời:

Tất cả các phát biểu trên đều đúng.

2. Thực hiện các hoạt động sau để tìm hiểu thêm về các góc so le, các góc đồng vị

a) Đọc và làm theo

- Vẽ một đường thẳng c cắt cả hai đường thẳng song song a và b (h.14)

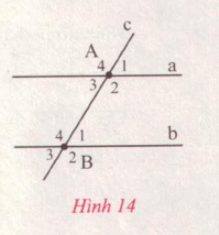
- Đo các cặp góc so le trong $\widehat{A_{3}}$ và $\widehat{B_{1}}$; $\widehat{A_{2}}$ và $\widehat{B_{4}}$. So sánh các cặp góc so le trong đó.

- Đo các cặp góc đồng vị $\widehat{A_{1}}$ và $\widehat{B_{1}}$; $\widehat{A_{2}}$ và $\widehat{B_{2}}$; $\widehat{A_{4}}$ và $\widehat{B_{4}}$. So sánh các cặp góc đồng vị đó.

- Đo các cặp góc trong cùng phía $\widehat{A_{3}}$ và $\widehat{B_{4}}$; $\widehat{A_{2}}$ và $\widehat{B_{1}}$. Cho biết tổng số đo của các cặp góc trong cùng phía đo.

Trả lời:

- Dùng thước đo độ để đo.

- So sánh ta có:

+ $\widehat{A_{3}}$ = $\widehat{B_{1}}$; $\widehat{A_{2}}$ = $\widehat{B_{4}}$

+ $\widehat{A_{1}}$ = $\widehat{B_{1}}$; $\widehat{A_{2}}$ = $\widehat{B_{2}}$; $\widehat{A_{4}}$ = $\widehat{B_{4}}$

+ $\widehat{A_{3}}$ + $\widehat{B_{4}}$ = 180$^{0}$; $\widehat{A_{2}}$ + $\widehat{B_{1}}$ = 180$^{0}$

b) Đọc kĩ nội dung sau

Nếu một đường thẳng cắt cả hai đường thẳng song song thì:

• Hai góc so le trong bằng nhau;
• Hai góc dồng vị bằng nhau;
• Hai góc trong cùng phía bù nhau.

c) Luyện tập

- Xem hình 15. Biết a // b và $\widehat{A_{4}}$ = 37$^{0}$.

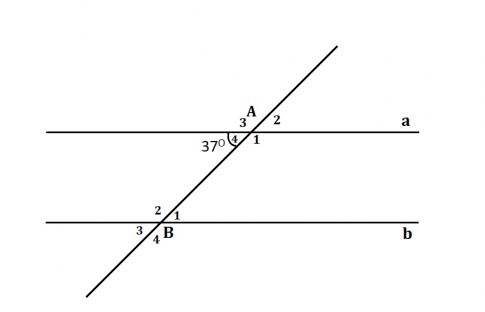
- Trả lời các câu hỏi sau:

+) Số đo góc B₃ bằng bao nhiêu độ?

+) So sánh hai góc A₁ và B₄.

+) Hãy cho biết số đo của góc B₂.

Trả lời:

+) Số đo góc B₃ bằng 37 độ vì góc A₄ và góc B₃ là hai góc đồng vị.

+) $\widehat{A_{1}}$ = $\widehat{B_{4}}$ vì hai góc này kề bù hai góc bằng nhau.

+) $\widehat{B_{2}}$ + $\widehat{B_{3}}$ = 180$^{0}$ $\Rightarrow$ $\widehat{B_{2}}$ = 180$^{0}$ - $\widehat{B_{3}}$ = 143$^{0}$.