A. Hoạt động khởi động

1. Mỗi số cho dưới đây thuộc tập hợp số nào trong các tập hợp số N, Z, Q?

a) $\frac{-17}{31}$;              b) 23;             c) 0;               d) 4,581.

Trả lời:

a) $\frac{-17}{31}$ $\in$ Q;              b) 23 $\in$ N, Z, Q;             c) 0 $\in$ N, Z, Q;               d) 4,581 $\in$ Q.

2. Có thể sử dụng loại số thích hợp nào để biểu thị trong mỗi tình huống sau?

a) Số học sinh của một trường đi tham quan, dã ngoại;

b) Chiều cao cửa ra/vào của lớp học;

c) Giá tiền của một chiếc xe máy;

d) Số ô tô tối thiểu cần có để chở hết 145 hành khách, biết rằng mỗi xe ô tô chỉ chở được không quá 40 người.

Trả lời:

a) Số tự nhiên;

b) Số thập phân hữu hạn;

c) Số tự nhiên;

d) Số tự nhiên.

3. Quan sát trục số sau và xác định xem các điểm A, B, C lần lượt biểu diễn các số hữu tỉ nào? Sau đó hãy viết các số hữu tỉ đó dưới dạng số thập phân.

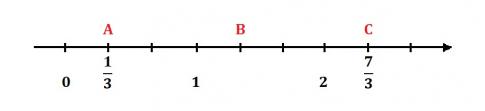
Trả lời:

Điểm A biểu diễn số $\frac{1}{3}$ = 0,(3);

Điểm B biểu diễn số $\frac{4}{3}$ = 1,(3);

Điểm C biểu diễn số $\frac{7}{3}$ = 2,(3).

B. Hoạt động hình thành kiến thức

1. Đọc nhận xét sau

• Mỗi số hữu tỉ được biểu diễn dưới dạng một số thập phân hữu hạn hoặc vô hạn tuần hoàn.

Ví dụ: $\frac{3}{20}$ = 0,15; -$\frac{17}{11}$ = -1,(54)

• Mỗi số vô tỉ dược biểu diễn dưới dạng một số thập phân vô hạn không tuần hoàn.

Ví dụ: $\sqrt{2}$ = 1,4142135623730950488016887...., là một số thập phân vô hạn không tuần hoàn. Vì thế, $\sqrt{2}$ là số vô tỉ.

Các số: $\sqrt{3}$; -$\sqrt{8}$; $\sqrt{11}$ cũng đều là số vô tỉ.

2. a) Đọc kĩ nội dung sau

• Số hữu tỉ và só vô tỉ được gọi chung là số thực.

Ví dụ: -3; $\frac{4}{5}$; -0,12; $\sqrt{3}$; 5$\frac{1}{3}$,... là những số thực.

• Tập hợp các số thực được kí hiệu là R.

b) Cách viết x $\in$ R cho ta biết điều gì?

Trả lời:

Cách viết này cho thấy x là một số thực.

c) Trong các câu sau, câu nào đúng, câu nào sai?

- Nếu a là số tự nhiên thì a không phải là số vô tỉ.

- Mọi số nguyên đều là số thực.

- Mọi số hữu tỉ đều là số thực.

- Số 0 vừa là số hữu tỉ vừa là số vô tỉ.

Trả lời:

Đ - Nếu a là số tự nhiên thì a không phải là số vô tỉ.

Đ - Mọi số nguyên đều là số thực.

Đ - Mọi số hữu tỉ đều là số thực.

S - Số 0 vừa là số hữu tỉ vừa là số vô tỉ.

3. a) Đọc kĩ nội dung sau

Trục số thực

• Trên trục số, có những điểm biểu diễn cho số hữu tỉ. Tuy nhiên, lại có những diểm trên trục số không biểu diễn cho bất kì mọt số hữu tỉ nào. Những điểm đó sẽ biểu diễn cho số vô tỉ.
• Mỗi điểm trên trục số đều biểu diễn một số thực. Vì thế trục số còn được gọi là số thực.
• Tập hợp các số thực lấp đầy trục số.

Trục số thực được vẽ như sau:

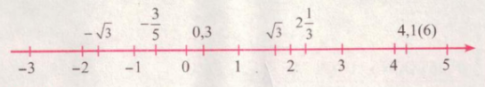
b) Chú ý

• Trong tập hợp các số thực cũng có các phép toán với các tính chất tượng tự như các phép toán trong tập hợp các số hữu tỉ.

4. a)  Hãy quan sát các hình vẽ sau:

b) Đọc kĩ nội dung sau

So sánh các số thực:

• Trên trục số thực, những số thực nào đứng bên phải số 0 thì được gọi là số thực dương và những số thực nào đứng bên trai số 0 thì đưuọc gọi là số thực âm.
• Trên trục số, nếu số thực x đứng bên trái số thực y thì ta nói rằng x nhỏ hơn y (kí hiệu là x < y) hay còn nói là y hơn hơn x (kí hiệu y > x).
• Với hai số thực bất kì, ta luôn có hoặc x = y, hoặc x > y, hoặc x < y.
• Vì số thực nào cũng có thể viết được dưới dạng số thập phân hữu hạn hoặc vô hạn ta có thể so sánh hai số thực theo như cách so sánh hai số hữu tỉ viết dưới dạng thập phân.

c) So sánh các cặp số thực:

+) 4,123 và 4,(3);                   +) 2,(35) và 2,3691215…

+) -3,45 và -3,5;                     +) -0,(63) và -$\frac{7}{11}$.

Trả lời:

+) 4,123 < 4,(3);                     +) 2,(35) < 2,3691215…

+) -3,45 > -3,5;                       +) -0,(63) = -$\frac{7}{11}$.

d) Điền các kí hiệu $\in$, $\notin$, $\subset$ thích hợp vào chỗ chấm:

3 … Q;                   3 … R;                    3 … I;                -2,53 … Q;

0,2(35) … I;             N … Z;                   I … R.

Trả lời: 

3 $\in$ Q;        3 $\in$ R;         3 $\notin$ I;        -2,53 $\in$ Q;

0,2(35) $\notin$ I;         N $\subset$ Z;             I $\subset$ R.