Giải VNEN toán hình 7 bài 8: Các trường hợp bằng nhau của tam giác vuông
Giải bài 8: Các trường hợp bằng nhau của tam giác vuông - Sách hướng dẫn học toán 7 tập 1 trang 143. Sách này nằm trong bộ VNEN của chương trình mới. Dưới đây sẽ hướng dẫn trả lời và giải đáp các câu hỏi trong bài học. Cách làm chi tiết, dễ hiểu, Hi vọng các em học sinh nắm tốt kiến thức bài học.
A. Hoạt động khởi động
1. Nhớ lại (sgk trang 143)
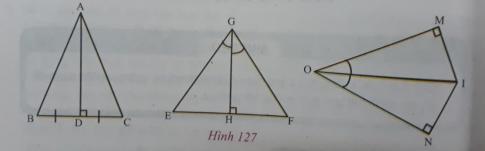
2. Hãy viết kí hiệu thể hiện sự bằng nhau của các cặp tam giác vuông có trên hình 127. Giải thích vì sao.
Trả lời:
+ $\bigtriangleup ADB = \bigtriangleup ADC$ (hai cạnh góc vuông) vì có: AD chung, BD = DC (giả thiết);
+ $\bigtriangleup GEH= \bigtriangleup GFH$ (cạnh góc vuông – góc nhọn kề cạnh đó) vì có: GH chung, $\widehat{HGE} = \widehat{HGF}$ (giả thiết);
+ $\bigtriangleup OIN = \bigtriangleup OIM$ (cạnh huyền – góc nhọn) vì có: OI chung, $\widehat{NOI} = \widehat{MOI}$ (giả thiết);
3. Quan sát hình 128 và đọc ví dụ sau (sgk trang 144)
B. Hoạt động hình thành kiến thức
1. a) Đọc kĩ nội dung sau (sgk trang 144)
b) Cho $\bigtriangleup ABC$ cân tại A. Kẻ AH vuông góc với BC (h.130). Chứng minh rằng $\bigtriangleup AHB = \bigtriangleup AHC$ (giải bằng hai cách).
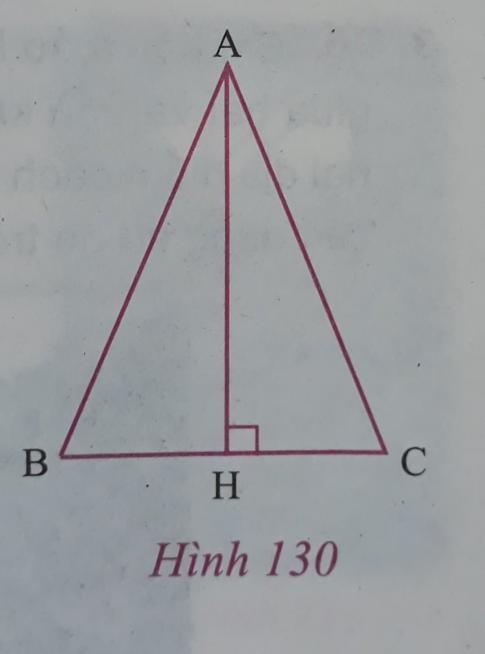
Gợi ý:
Cách 1: (sgk trang 145)
Trả lời:
Cách 2:
Xét $\bigtriangleup AHB$ và $\bigtriangleup AHC$ có:
AB = AC (giả thiết);
$\widehat{B} = \widehat{C}$ (do tam giác ABC cân tại A);
$\Rightarrow $ $\bigtriangleup AHB = \bigtriangleup AHC$ (cạnh huyền – góc nhọn);



Bình luận