Đề số 5: Đề kiểm tra toán 8 Kết nối bài 39 Hình chóp tứ giác đều
III. DẠNG 3 – ĐỀ TRẮC NGHIỆM VÀ TỰ LUẬN
ĐỀ 5
I. Phần trắc nghiệm (4 điểm)
Câu 1: Một hình chóp tứ giác đều có thể tích bằng $200 cm^{3}$, chiều cao bằng 12 cm. Tính độ dài cạnh bên.
A. 12 cm
B. 13 cm
C. 11 cm
D. 16 cm
Câu 2: Chọn khẳng định sai: Cho hình chóp tứ giác đều. Khi đó:
A. Đáy là hình vuông
B. Có 4 mặt bên
C. Có tất cả 8 cạnh
D. Số mặt của hình chóp là 4.
Câu 3: Cho hình vẽ sau đây
Cho AM = 5cm, MN = 4cm. Tìm độ dài các cạnh bên của hình
A. AN = AP = AQ = 4cm.
B. AN = AP = AQ = 5cm.
C. AN = AP = AQ = 1cm.
D. AN = AP = AQ = 9cm.
Câu 4: Cho hình chóp tứ giác đều có tất cả các mặt đều là tam giác đều có diện tích xung quanh là và chiều cao của hình chóp bằng 7m. Tính thể tích của hình chóp
A. $210 m^{3}$
B. $630 m^{3}$
C. $70 m^{3}$
D. $30 m^{3}$
II. Phần tự luận (6 điểm)
Câu 1 (6 điểm): Một hình chóp tứ giác đều S.ABCD có cạnh bên SA = 13cm và độ dài cạnh đáy là $5\sqrt{2}$. Tính thể tích của hình chóp tứ giác đều.
Trắc nghiệm: (Mỗi câu đúng tương ứng với 1 điểm)
Câu hỏi | Câu 1 | Câu 2 | Câu 3 | Câu 4 |
Đáp án | B | D | B | C |
Tự luận:
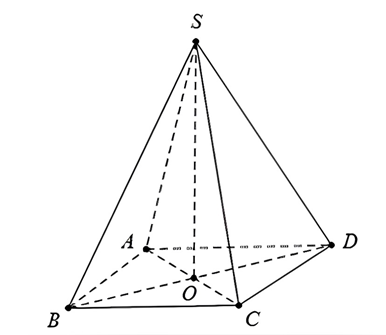
Gọi O là giao điểm của AC và BD.
Áp dụng định lí Pytago vào tam giác vuông ABC có:
$AC^{2}=AB^{2}+BC^{2}=(5.\sqrt{2})^{2}+(5.\sqrt{2})^{2}=100$
$=> AC=10cm; AO=\frac{1}{2}AC=5cm$
Áp dụng định lí Pytago vào tam giác vuông SAO có:
$SO^{2}=SA^{2}-AO^{2}=13^{2}-5^{2}=144 $
$=> SO=12cm$
Diện tích đáy là: $(5.\sqrt{2})^{2}=50cm^{2}$
Vậy $V=\frac{1}{3}.50.12=200cm^{3}$
Giải những bài tập khác
Giải bài tập những môn khác
Giải sgk lớp 8 cánh diều
Giải SBT lớp 8 kết nối tri thức
Giải SBT lớp 8 chân trời sáng tạo
Soạn SBT lớp 8 cánh diều
Trắc nghiệm 8 Kết nối tri thức
Trắc nghiệm 8 Chân trời sáng tạo
Trắc nghiệm 8 Cánh diều
Bộ đề thi, đề kiểm tra lớp 8 chân trời sáng tạo
Giáo án lớp 8
Bình luận