Đề số 4: Đề kiểm tra toán 8 Kết nối bài 11 Hình thang cân
ĐỀ 4
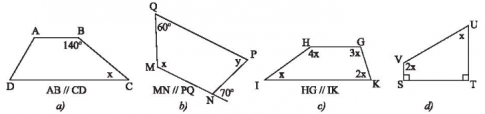
Câu 1 (6 điểm). Tìm x và y ở các hình sau.
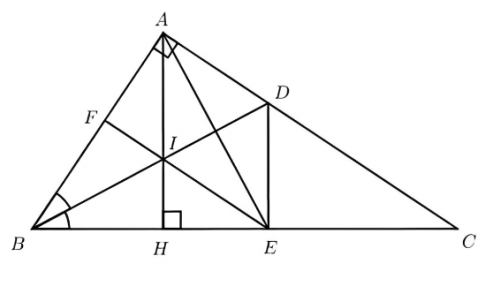
Câu 2 (4 điểm). Cho tam giác ABC vuông tại A (AB < AC). Tia phân giác của góc B cắt AC tại D. Trên BC lấy điểm E sao cho BE = BA.
a) Chứng minh rằng: ΔABD = ΔEBD
b) Kẻ đường cao AH của tam giác ABC. Chứng mình rằng tứ giác ADEH là hình thang vuông.
Câu 1
a) $x=180^{\circ} -140^{\circ} = 40^{\circ}$
b) $x=180^{\circ}- 60^{\circ}= 120^{\circ}$
$MN // PQ$ => y = góc N ngoài = $70^{\circ}$ (so le trong)
Câu 2
a) Xét ΔABD và ΔEBD ta có:
AB = BE (gt)
BD là cạnh chung
$\widehat{ABD} = \widehat{DBE}$ (BD là tia phân giác của góc B)
=> $\Delta ABD = \Delta EBD(c.g.c)$
b) Ta có: $\widehat{DEB} = \widehat{BAD}(\Delta EBD = \Delta ABD)$
Mà $\widehat{BAD}=90^{\circ}$ ($\Delta ABD$ vuông tại A)
=>$ \widehat{DEB}=90^{\circ}$
=> $DE\perp BC$
mà $AH\perp BC$ (gt)
=> DE // AH
= >Tứ giác ADEH là hình thang
Lại có $\widehat{AHE} = 90^{\circ} (AH\perp BC)$
Vậy tứ giác ADEH là hình thang vuông.
Xem toàn bộ: Đề kiểm tra Toán 8 KNTT bài 11: Hình thang cân

Bình luận