Đề số 3: Đề kiểm tra toán 8 Kết nối bài 11 Hình thang cân
II. DẠNG 2 – ĐỀ KIỂM TRA TỰ LUẬN
ĐỀ 3
Câu 1 (6 điểm). Cho hình thang cân ABCD có AB//CD. Chứng minh $\widehat{ADB}=\widehat{BCA}$
Câu 2 (4 điểm). Cho tam giác nhọn ABC có AH là đường cao. Tia phân giác của góc B cắt AC tại M. Từ M kẻ đường thẳng vuông góc với AH cắt AB tại N.
a) Chứng minh rằng tứ giác BCMN là hình thang.
b) Chứng mình rằng BN = MN.
Câu 1:
Có ABCD là hình thang cân
$=> AD=BC, \widehat{DAB}=\widehat{CBA}$
Xét tam giác ADB và tam giác BCA, ta có:
$AD=BC$
$\widehat{DAB}=\widehat{CBA}$
AB chung
=> tam giác ADB = tam giác BCA (c.g.c)
=> góc ADB = góc BCA (2 góc tương ứng)
Câu 2:
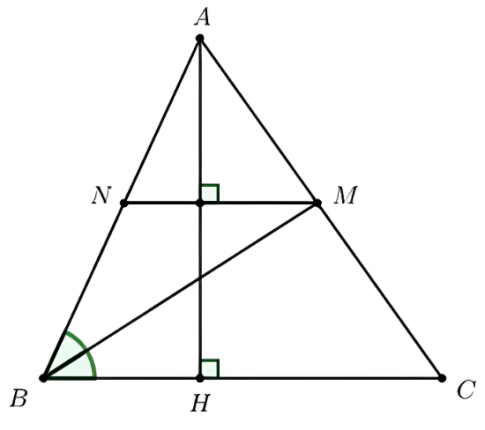
a) Ta có: $MN\perp AH$ (gt)
Và $BC\perp AH$ (AH là đường cao của tam giác ABC)
=> MN // BC
=> BCMN là hình thang
b) $\widehat{NBM}=\widehat{MBC}$ (BM là tia phân giác góc B)
=> $\widehat{BMN}=\widehat{NBM}$
=> ΔBMN cân tại N.
=> BN = MN
Xem toàn bộ: Đề kiểm tra Toán 8 KNTT bài 11: Hình thang cân
Giải những bài tập khác
Giải bài tập những môn khác
Giải sgk lớp 8 cánh diều
Giải SBT lớp 8 kết nối tri thức
Giải SBT lớp 8 chân trời sáng tạo
Soạn SBT lớp 8 cánh diều
Trắc nghiệm 8 Kết nối tri thức
Trắc nghiệm 8 Chân trời sáng tạo
Trắc nghiệm 8 Cánh diều
Bộ đề thi, đề kiểm tra lớp 8 chân trời sáng tạo
Giáo án lớp 8
Bình luận